This set of Powder Metallurgy Multiple Choice Questions & Answers (MCQs) focuses on “Particle Size Measurement Techniques”.
1. Stoke’s law can be represented by which of the following equation?
a) V=(ρp – ρf)d3g/18η
b) V=(ρp – ρf)d2g/18η
c) V=(ρf – ρp)d2g/18η
d) V=(ρp – ρf)d2/18ηg
View Answer
Explanation: Stoke’s law which states that the settling velocity of falling spherical particles at low velocity in a quiescent homogenous fluid of infinite extent is proportional to the square of the particle diameter, can be represented by the equation V=(ρp – ρf) d2g/18η where, V is the terminal velocity of the particle in cm/sec, ρf and ρp are the density of fluid and particle respectively in gm/cc, d is the diameter of particle in cm, g is the gravitational acceleration in cm/sec2 and η is the viscosity of fluid in poises.
2. Reynold number can be expressed as R=Vdρf/η.
a) True
b) False
View Answer
Explanation: Reynold number is used to determine whether the flow is turbulent or laminar where, V is the terminal velocity of the particle in cm/sec, ρf is the density of fluid in gm/cc, d is the diameter of particle in cm and η is the viscosity of fluid in poises.
3. Which of the following is a fractionation method for sizing by sedimentation method?
a) Hydrometer method
b) Pipette method
c) Sedimentation and decantation method
d) Turbidimetry
View Answer
Explanation: Sedimentation and decantation method is a fractionation method for sizing by sedimentation method whereas hydrometer method, pipette method and turbidimetry are non-fractionation methods which are used for determining size distribution and estimating specific surface.
4. Which system of sieves is used in Germany?
a) DIN system
b) B.S. system
c) AFNOR system
d) Tyler system
View Answer
Explanation: Different systems of sieves are used in various countries for the determination of sieve size powders. In Germany usually the DIN system, in U.K mainly the B.S. system, in France the AFNOR system and in America the Tyler system is widely prevalent.
5. ____ particles are smaller than 44-micron but greater than 1-micron aperture.
a) Sieve
b) Sub-sieve
c) Sub-micron
d) Ultra-fine
View Answer
Explanation: The particles having size > 44-micron fall in the category of sieve class. Sub-sieve particles are smaller than 44-micron but greater than 1-micron aperture, and the sub-micron or ultra-fine powder particle size is smaller than 1-micron.
6. Which of the following are the techniques for particle size measurement?
a) Macroscopic analysis
b) Sieve analysis and Absorption method
c) Sieve analysis, microscopic analysis, sedimentation method, and permeability method
d) Filtration method and Sieve analysis
View Answer
Explanation: There are 7 particle size measurement technique which are as follows: Sieving analysis, Microscopic analysis, Sedimentation method, Elutriation method, Permeability method, Adsorption method and Electrolytic Resistivity method.
7. The particle size measurement technique based on the settling velocity of particles in stationary fluid medium is called _____
a) Sedimentation Method
b) Microscopic Method
c) Elutriation Method
d) Permeability Method
View Answer
Explanation: Sedimentation method is based on the settling velocity of particles in stationary fluid medium whereas, elutriation differs from sedimentation in that the fluid is in motion in the upward direction against the falling particles. Microscopic method involves actual counting of particles. The permeability method involves measuring the pressure drop across the bed of packed powder particles contained in a chamber in relation to the fluid flow.
8. _______ is the statistical relation between amount and size.
a) Particle size distribution
b) Cumulative weight retained
c) Particle size
d) Packing density
View Answer
Explanation: Particle size distribution is the statistical relation between amount and size. It is also of fundamental importance as it affects the pressing and sintering behavior as well as the physical and mechanical properties of the sintered material.
9. _______ establishes the relationship between the settling velocity of falling particles and particle size.
a) Hess law
b) Continuity equation
c) Stoke’s law
d) Bernoulli’s equation
View Answer
Explanation: Stoke’s law establishes the relationship between the settling velocity of falling particles and particle size which states that the settling velocity of falling spherical particles at low velocity in a quiescent homogenous fluid of infinite extent is proportional to the square of the particle diameter.
10. The laboratory methods for sizing by _________ can be divided into fractionating and non-fractionation groups.
a) Elutriation method
b) Sedimentation method
c) Adsorption method
d) Permeability method
View Answer
Explanation: The laboratory methods for sizing by sedimentation can be divided into 2 groups: (1) The fractionating methods are employed when it is essential to separate individual size fractions for individual examinations. (2) Non-fractionation methods are used for determining size distribution and estimating specific surface.
11. In Tyler standard screen scale, sieve series having a ratio of ______ is used.
a) \(\sqrt{3}\) : 1
b) \(\sqrt{2}\) : 1
c) \(\sqrt{2}\) : 2
d) \(\sqrt[4]{3}\) : 1
View Answer
Explanation: In Tyler standard screen scale, the width of each consecutive opening is exactly \(\sqrt{2}\) times the width of the previous sieve and hence the area of openings is doubled from the next finer sieve. If a closer sizing is required, an expanded sieve series having the ratio of \(\sqrt[4]{2}\):1 is used in which each and every sieve is a part of their \(\sqrt{2}\) series.
12. ________ is the particle size through square grid method where magnification of the objective is x10.

a) 0.259 mm
b) 0.282 mm
c) 0.156 mm
d) 2.963 mms
View Answer
Explanation: In optical microscopy, there are two objective lens and one of them contain a square grid (16×16) and area of each square is 0.25m2. We can calculate the particle size using this square grid where we have to count the number of 100%, 75%, 50% and 25% squares and then using the below formula we obtain the particle size.
d=\(\frac{\sqrt{x}}{\sqrt{\pi \times magnification \, of \, objective}}\) where, x=Number of squares x Area of 1 square and d=particle diameter
Thus, from the above figure: 100% square=6; 75% square=2; 50% square=4 and 25% square=2. Hence, x=10 x 0.25=2.5. Therefore, d=\(\frac{\sqrt{2.5}}{\sqrt{\pi \times 10}}\)=0.282mm.
13.________ is the particle size through linear/ horizontal scale method where magnification of the objective is x10.
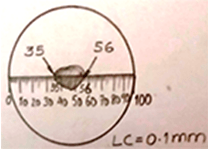
a) 0.21mm
b) 2.10mm
c) 0.20mm
d) 0.22mm
View Answer
Explanation: The formula to calculate particle diameter (d) is given by:
d=\(\frac{number \, of \, division \times L.C}{magnification \, of \, objective}\) where, number of division=last – start point and L.C=least count=0.1mm
Thus, from the above figure: number of division=56-35=21
Hence, d=\(\frac{21 \times 0.1}{10}\)=0.21mm.
14. The below figure represents the relative size distribution graph.
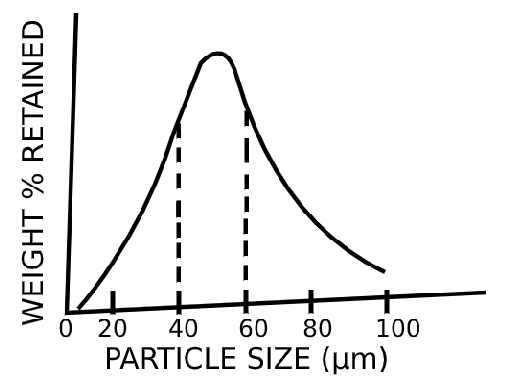
a) True
b) False
View Answer
Explanation: The above figure represents the relative size distribution graph which is a curve between % weight retained and particle size(μm). This curve represents a narrow particle size distribution because of narrow peak and thus particles have a close size range (40-60 μm).
Sanfoundry Global Education & Learning Series – Powder Metallurgy.
To practice all areas of Powder Metallurgy, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Mechanical Engineering Books
- Apply for Mechanical Engineering Internship
- Practice Metallurgical Engineering MCQs
- Practice Mechanical Engineering MCQs
- Check Powder Metallurgy Books
