This set of Linear Integrated Circuit Multiple Choice Questions & Answers (MCQs) focuses on “Triangular and Sawtooth Wave Generator”.
1. How a triangular wave generator is derived from square wave generator?
a) Connect oscillator at the output
b) Connect Voltage follower at the output
c) Connect differential at the output
d) Connect integrator at the output
View Answer
Explanation: The output waveform of the integrator is triangular, if its input is square wave. Therefore, a triangular wave generator can be obtained by connecting an integrator at the output of the square wave generator.
2. The increase in the frequency of triangular wave generator.
a) Ramp the amplitude of triangular wave
b) Increase the amplitude of triangular wave
c) Decrease the amplitude of triangular wave
d) None of the mentioned
View Answer
Explanation: As the resistor value increase or decrease, the frequency of triangular wave will decrease or increase, respectively. Therefore, the amplitude of the triangular wave decreases with an increase in it frequency and vice verse.
3. Which among the following op-amp is chosen for generating triangular wave of relatively higher frequency?
a) LM741 op-amp
b) LM301 op-amp
c) LM1458 op-amp
d) LM3530 op-amp
View Answer
Explanation: The frequency of the triangular wave generator is limited by the slew rate of the op-amp. LM301 op-amp has a high slew rate.
4. What is the peak to peak (PP) output amplitude of the triangular wave?
a) VO(pp) = + VRamp + (- VRamp)
b) VO(pp) = – VRamp + (+ VRamp)
c) VO(pp) = + VRamp – (- VRamp)
d) VO(pp) = – VRamp – (+ VRamp)
View Answer
Explanation: The peak to peak output waveform, VO(pp) = + VRamp-(-VRamp)
Where, – VRamp –> Negative going ramp ;
+ VRamp–> positive going ramp.
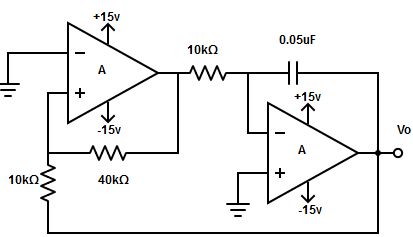
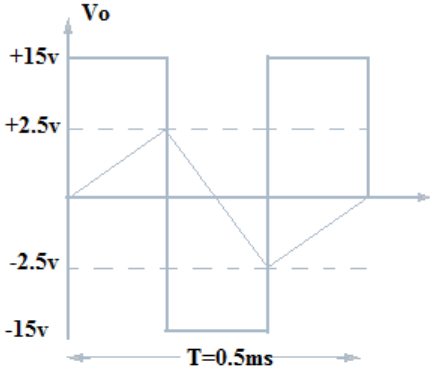
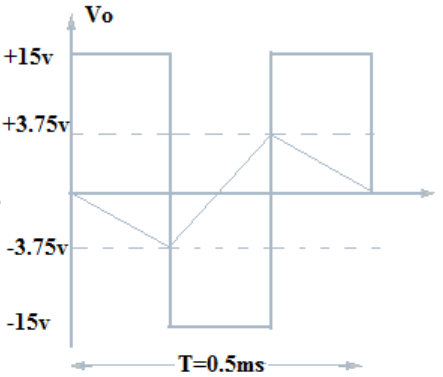
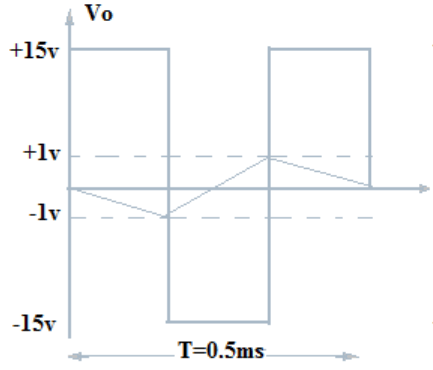
5. Determine the output triangular waveform for the circuit.
a)
b)
c)
d)
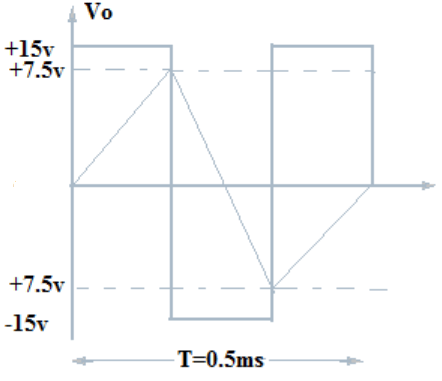
View Answer
Explanation: The voltage at which A1 switch from +Vsat to -Vsat
=> -Vramp =(-R2 / R3) × (+Vsat)
= (-10kΩ/40kΩ) ×15v =-3.75v
Similarly, the voltage at which A1 switch from -Vsat to +Vsat
=> +Vramp = (-R2 / R3) × (-Vsat)
= 10kΩ/40kΩ ×15v =3.75v
∴ Time period, T = (4R1C1R2) / R3
= (4×10kΩ×0.05µF×10kΩ) /40kΩ = 0.5 ms.
6. Find the capacitor value for a the output frequency, fo = 2kHz & VO(pp) = 7v, in a triangular wave generator. The op-amp is 1458/741 and supply voltage = ±15v. (Take internal resistor=10kΩ)
a) 0.03nF
b) 30nF
c) 0.3nF
d) 3nF
View Answer
Explanation: Given, Vsat =15v
∴ VO(pp) = (2R2/R3) × Vsat
=> R2 =(VO(pp) ×R3) / (Vsat×2) = [7/(2×15)]×R3 = 0.233R3
∵ Internal resistor, R2 = R1= 10kΩ
=> R3 = 0.233×10kΩ = 2.33kΩ.
So, the output frequency fO = R3 / ( 4×R1 ×C1× R2)
=> 2khz = 2.33khz/ (4×10kΩ ×10kΩ×C1)
=> C1 = 2.33kΩ / (8×10-11) = 2.9 ×10-9 ≅3nF.
7. Triangular wave form has
a) Rise time < fall time
b) Rise time = fall time
c) Rise time ≥ fall time
d) None of the mentioned
View Answer
Explanation: The triangular wave form has rise time of the triangular wave always equal to its fall time, that is, the same amount of time is required for the triangular wave to swing from -VRamp to +VRamp as from +VRamp to -VRamp.
8. Output of an integrator producing waveforms of unequal rise and fall time are called
a) Triangular waveform
b) Sawtooth waveform
c) Pulsating waveform
d) Spiked waveform
View Answer
Explanation: Sawtooth waveform has unequal rise and fall times. It may rise positively many times faster than it falls negatively or vice versa.
9. Find out the sawtooth wave generator from the following circuits.
a)
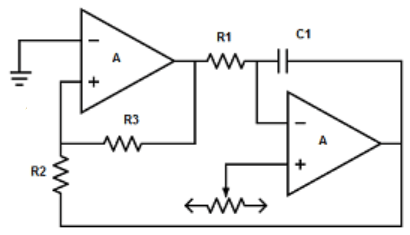
b)
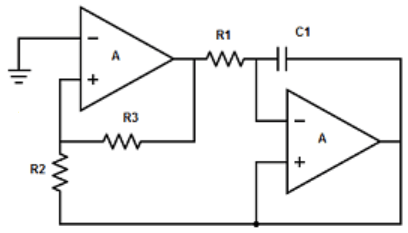
c)
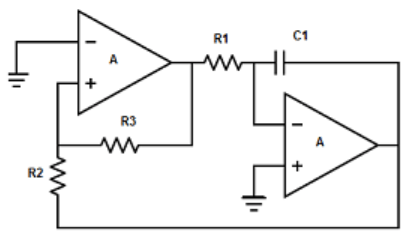
d) None of the mentioned
View Answer
Explanation: The triangular wave generator can be converted into a sawtooth wave generator by inserting a variable dc voltage into the non-inverting terminal of the integrator.
10. Consider the integrator used for generating sawtooth wave form. Match the list I with the list II depending on the movement of wiper.
| List-I | List-II |
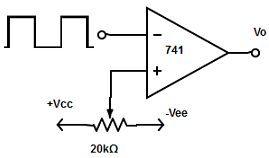 |
Rise time =fall time (Triangular wave) |
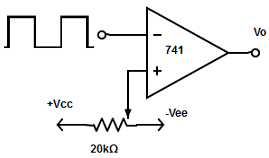 |
Longer fall time and short rise time (Sawtooth wave) |
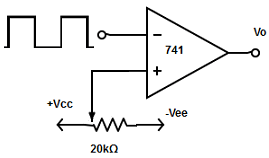 |
Longer rise time and short fall time (Sawtooth wave) |
a) 1-iii, 2-ii, 3-i
b) 1-i, 2-ii, 3-iii
c) 1-i, 2-iii, 3-ii
d) 1-ii, 2-iii, 3-i
View Answer
Explanation: Depending on the duty cycle (movement of the wiper) the type of waveform is determined.
Sanfoundry Global Education & Learning Series – Linear Integrated Circuits.
To practice all areas of Linear Integrated Circuits, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
