This set of Linear Integrated Circuit Multiple Choice Questions & Answers (MCQs) focuses on “First & Second Order High Pass Butterworth Filter and Higher Order Filters”.
1. How is the higher order filters formed?
a) By increasing resistors and capacitors in low pass filter
b) By decreasing resistors and capacitors in low pass filter
c) By inter changing resistors and capacitors in low pass filter
d) All of the mentioned
View Answer
Explanation: High pass filter are often formed by interchanging frequency determining resistors and capacitors in low pass filters. For example, a first order high pass filter is formed from a first order low pass filter by inter changing components Rand C.
2. In a first order high pass filter, frequencies higher than low cut-off frequencies are called
a) Stop band frequency
b) Pass band frequency
c) Centre band frequency
d) None of the mentioned
View Answer
Explanation: Low cut-off frequency, fL is 0.707 times the pass band gain voltage. Therefore, frequencies above fL are pass band frequencies.
3. Compute the voltage gain for the following circuit with input frequency 1.5kHz.
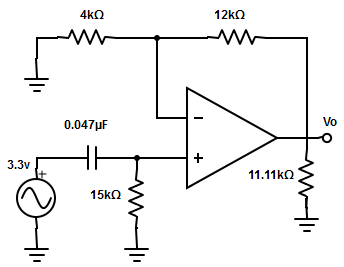
a) 4dB
b) 15dB
c) 6dB
d) 12dB
View Answer
Explanation: |VO/Vin|= [AF×(f/fL)]/ [√1+(f/fL)2] = [4×(1.5kHz/225.86)] / √[1+(1.5kHz/225.86)2] =26.56/6.716=3.955 =20log(3.955)=11.9.
|VO/Vin|≅12 dB
AF= 1+(RF /R1)= 1+(12kΩ/4kΩ) =4.
fL= 1/(2πRC) = 1/2π×15kΩ×0.047µF= 1/4.427×10-3 =225.86Hz.
4. Determine the expression for output voltage of first order high pass filter?
a) VO = [1+(RF /R1)]× [(j2πfRC/(1+j2πfRC)] × Vin
b) VO = [-(RF /R1)]× [(j2πfRC/(1+j2πfRC)] × Vin
c) VO = {[1+(RF /R1)]× /[1+j2πfRC] }× Vin
d) None of the mentioned
View Answer
Explanation: The first order high pass filter uses non-inverting amplifier. So, AF= 1+(RF /R1) and the output voltage, VO = [1+(RF /R1)]× [(j2πfRC/(1+j2πfRC)]× Vin.
5. The internal resistor of the second order high pass filter is equal to 10kΩ. Find the value of feedback resistor?
a) 6.9kΩ
b) 5.86kΩ
c) 10kΩ
d) 12.56kΩ
View Answer
Explanation: Pass band gain for second order butterworth response, AF =1.586.
=> AF= [1+(RF/R1)] => RF= (AF-1)×R1 =(1.586-1)×10kΩ =5860 =5.86kΩ.
6. Consider the following circuit and calculate the low cut-off frequency value?
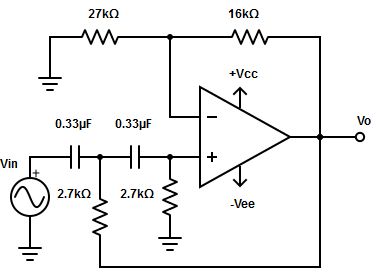
a) 178.7Hz
b) 89.3Hz
c) 127.65Hz
d) 255.38Hz
View Answer
Explanation: The low cut-off frequency for the given filter is fL =1/√[2π√(R2×R3×C2×C3)]=178.7Hz.
7. Determine voltage gain of second order high pass butterworth filter.
Specifications R3 =R2=33Ω, f=250hz and fL=1khz.
a) -11.78dB
b) -26.51dB
c) -44.19dB
d) None of the mentioned
View Answer
Explanation: Since R3 =R2
=> C2 = 1/(2π ×fL×R2) = 1/(2π ×1kHz×33Ω)
=> C3 =C2= 4.82µF.
Voltage gain of filter |VO/Vin|=AF / [√ 1+(fL/f)4] = 1.586/[1+(1kHz/250kz)4] =1.586/252=6.17×10-3 =20log(6.17×10-3)= -44.19dB.
8. From the given specifications, determine the value of voltage gain magnitude of first order and second order high pass butterworth filter?
Pass band voltage gain=2;
Low cut-off frequency= 1kHz;
Input frequency=500Hz.
a) First order high pass filter =-4.22dB , Second order high pass filter=-0.011dB
b) First order high pass filter =-0.9688dB , Second order high pass filter=-6.28dB
c) First order high pass filter =-11.3194dB , Second order high pass filter=-9.3257dB
d) First order high pass filter =-7.511dB , Second order high pass filter=-5.8999dB
View Answer
Explanation: For first order high pass filter,
|VO/Vin|=AF ×(f/fL) / [ √1+(f/fL)2] =(2×(500Hz/1kHz)) /√[1+(500Hz/1kHz)2] => |VO/Vin| = 1/1.118= 0.8944 =20log(0.8944) =-0.9686dB.
For second order high pass filter,
|VO/Vin|=AF / [ √ 1 +(fL/f)4] =2/√[1+ (1kHz/500Hz)2] =>|VO/Vin|=2/4.123= =0.4851 = 20log(0.4851) = -6.28dB.
9. How is the higher order filters formed?
a) Using first order filter
b) Using second order filter
c) Connecting first and second order filter in series
d) Connecting first and second order filter in parallel
View Answer
Explanation: Higher filters are formed by using the first and second order filters. For example, a third order low pass filter is formed by cascading first and second order low pass filter.
10. State the disadvantage of using higher order filters?
a) Complexity
b) Requires more space
c) Expensive
d) All of the mentioned
View Answer
Explanation: Although higher order filter than necessary gives a better stop band response, the higher order type is more complex, occupies more space and is more expensive.
11. The overall gain of higher order filter is
a) Varying
b) Fixed
c) Random
d) None of the mentioned
View Answer
Explanation: The overall gain of higher order filter is fixed because all the frequency determining resistor and capacitors are equal.
12. Find the roll-off rate for 8th order filter
a) -160dB/decade
b) -320dB/decade
c) -480dB/decade
d) -200dB/decade
View Answer
Explanation: For nth order filter the roll-off rate will be -n×20dB/decade.
=>∴ for 8th order filter= 8×20=160dB/decade.
Sanfoundry Global Education & Learning Series – Linear Integrated Circuits.
To practice all areas of Linear Integrated Circuits, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
