This set of Linear Integrated Circuit Multiple Choice Questions & Answers (MCQs) focuses on “Band Pass Filter”.
1. Which filter attenuates any frequency outside the pass band?
a) Band-pass filter
b) Band-reject filter
c) Band-stop filter
d) All of the mentioned
View Answer
Explanation: A band- pass filter has a pass band between two cut-off frequencies fH and fL. So, any frequency outside this pass band is attenuated.
2. Narrow band-pass filters are defined as
a) Q < 10
b) Q = 10
c) Q > 10
d) None of the mentioned
View Answer
Explanation: Quality factor (Q) is the measure of selectivity, meaning higher the value of Q, the narrower its bandwidth.
3. A band-pass filter has a bandwidth of 250Hz and center frequency of 866Hz. Find the quality factor of the filter?
a) 3.46
b) 6.42
c) 4.84
d) None of the mentioned
View Answer
Explanation: Quality factor of band-pass filter, Q =fc/bandwidth= 566/250=3.46.
4. Find the center frequency of wide band-pass filter
a) fc= √(fh ×fL)
b) fc= √(fh +fL)
c) fc= √(fh -fL)
d) fc= √(fh /fL)
View Answer
Explanation: In a wide band-pass filter, the product of high and low cut-off frequency is equal to the square of center frequency
i.e. ( fc)2 =fH×fL
=> fc= √(fh×fL).
5. Find out the voltage gain magnitude equation for the wide band-pass filter.
a) AFt×( f/fL)/√[(1+(f/fh)2]×[1+(f/fL)2].
b) AFt/ √{[1+(f/fh)2]×[1+(f/fL)2]}
c) AFt/ √{[1+(f/fh)2]/[1+(f/fL)2]}
d) [AFt/(f/fL)]/ √{[1+(f/fh)2]/[1+(f/fL)2]}
View Answer
Explanation: The voltage gain magnitude of the band-pass filters equal to the product of the voltage gain magnitudes of high pass and low pass filter.
6. When a second order high pass filter and second order low pass sections are cascaded, the resultant filter is a
a) ±80dB/decade band-pass filter
b) ±40dB/decade band-pass filter
c) ±20dB/ decade band-pass filter
d) None of the mentioned
View Answer
Explanation: The order of the band-pass filter depends on the order of the high pass and low pass filter sections.
7. Find the voltage gain magnitude of the wide band-pass filter?
Where total pass band gain is=6, input frequency = 750Hz, Low cut-off frequency =200Hz and
high cut-off frequency=1khz.
a) 13.36 dB
b) 12.25 dB
c) 11.71 dB
d) 14.837dB
View Answer
Explanation: Voltage gain of the filter,
|VO/Vin|=[AFt×(f/fL)]/{√[1+(f/fL)2]×[1+f/fL)2]} =[6×(750/20)]/√{[1+(750/200)2]×[1+(750/200)2]}
=22.5/√(15.6×1.56) =5.519.
|VO/Vin|= 20log(5.519) =14.837dB.
8. Compute the quality factor of the wide band-pass filter with high and low cut-off frequencies equal to 950Hz and 250Hz.
a) 0.278
b) 0.348
c) 0.696
d) 0.994
View Answer
Explanation: Quality factor Q=√(fh×fL)/(fh-fL) = √(950Hz×250Hz)/(9950Hz-250Hz) =0.696.
9. The details of low pass filter sections are given as fh =10kHz, AF= 2 and f=1.2kHz. Find the voltage gain magnitude of first order wide band-pass filter, if the voltage gain magnitude of high pass filter section is 8.32dB.
a) 48.13dB
b) 10.02dB
c) 14.28dB
d) 65.99dB
View Answer
Explanation: |VO/Vin|(high pass filter) = 8.32dB=10(8.32/20) =2.606.
Therefore, the voltage gain of wide band-pass filter |VO/Vin|= AFt×(f/fL)/√[1+(f/fh)2)]×[1+(f/fL)2)] ={Af/√[(1+(f/fh)2]}×{(Af×f/fL)/√[1+(f/fL)2]} =Aft /√[1+(f/fh)2]×(2.606)
= [2/√(1+(1.2kHz/10kHz)2]×( 2.606) = 1.986×2.606 =5.17 =20log×(5.17) =14.28dB.
10. The quality factor of a wide band-pass filter can be
a) 12.6
b) 9.1
c) 14.2
d) 10.9
View Answer
Explanation: A wide band-pass filter has quality factor less than 10.
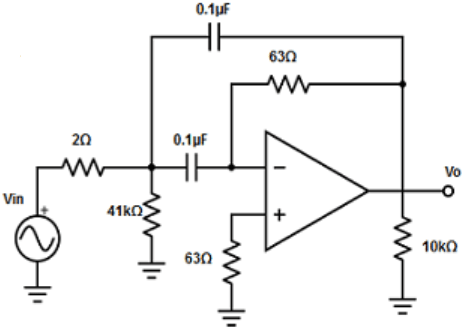
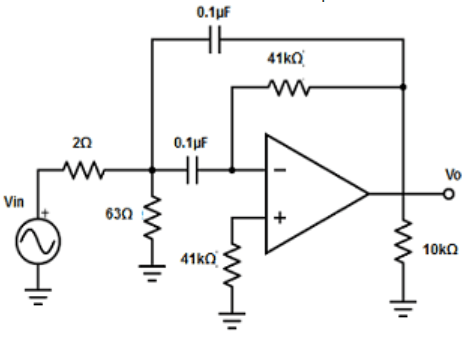
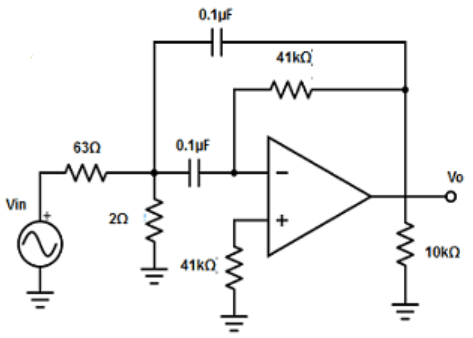
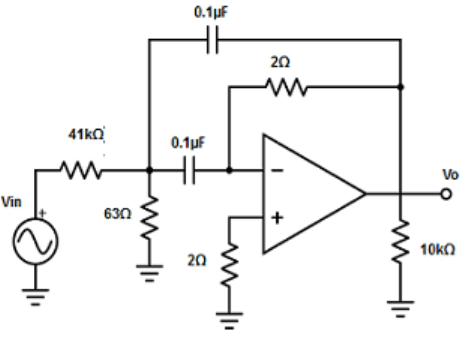
11. Design a narrow band-pass filter, with fc=1kHz, Q= 13 and AF=10 (Take C=0.1µF)
a)
b)
c)
d)
View Answer
Explanation: Given C =0.1µF.
Therefore, C1=C2 =0.1µF.
R1 =Q/(2π×fc×CAF) =13/( 2π×1kHz×0.1µF×10) =13/6.28 = 2.07 ≅ 2Ω.
R2 =Q/{2π×fc×C ×[(2Q2)- AF]} =13/{(2π×1kHz×0.1µF×[2×(132)-10]} = 13/0.2059=63.11 ≅ 63Ω.
R3 =Q/(π×fc×C) = 13/(π×1kHz×0.1µF) = 13/3.14×10-4 =41.40kΩ ≅41kΩ.
12. If the gain at center frequency is 10, find the quality factor of narrow band-pass filter
a) 1
b) 2
c) 3
d) None of the mentioned
View Answer
Explanation: The gain of the narrow band-pass filter must satisfy the condition, AF= 2×Q2
When Q=3,
=> 2×Q2 =2×(32) =18.
=> 10<18. Hence condition is satisfied when Q=3.
13. The advantage of narrow band-pass filter is
a) fc can be changed without changing gain
b) fc can be changed without changing bandwidth
c) fc can be changed without changing resistors
d) All of the mentioned
View Answer
Explanation: As the narrow band-pass filter has multiple filters. The center frequency can be changed to a new frequency without changing the gain or bandwidth and is accomplished by changing the resistor to a new value which is given as
R’=R×(fL/fc)2.
Sanfoundry Global Education & Learning Series – Linear Integrated Circuits.
To practice all areas of Linear Integrated Circuits, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Apply for Electrical Engineering Internship
- Practice Electronics & Communication Engineering MCQs
- Check Linear Integrated Circuits Books
- Practice Electrical Engineering MCQs
- Apply for Electronics & Communication Engineering Internship
