Merge Sort in Java | Merge Sort Program in Java

What is Merge Sort?

Merge Sort in Java is a divide and conquer-based sorting algorithm. In this sorting algorithm the unsorted array keeps on dividing into two halves until the array is either empty or contains only one element, which is the base case of Merge Sort, and then the halves are combined/Merged in sorted order producing a sorted array. It is one of the most popular and efficient sorting techniques.

Merge Sort Algorithm

Start
1. Declare Array, left, right and mid variables
2. Find mid by formula mid = (left+right)/2
3. Call MergeSort for the left to mid
4. Call MergeSort for mid+1 to right
5. Continue step 2, 3, and 4 while the left is less than the right
6. Then Call the Merge function
End

Problem Description

Write a Java Program to Implement Merge Sort on n Numbers Without tail-recursion.

Problem Solution

Divide the array into two equal parts. Recursively sort the two parts of the array and finally merge them.

Example:

Program/Source Code

Here is the source code of the Java Program to Implement Merge Sort on n Numbers Without tail-recursion. The program is successfully compiled and tested using IDE IntelliJ Idea in Windows 7. The program output is also shown below.

```
 
```

//Java Program to Implement Merge Sort on n Numbers Without tail-recursion

```
 
```
```
import java.io.BufferedReader;
```
```
import java.io.InputStreamReader;
```
```
import java.util.Arrays;
```
```
 
```
```
public class MergeSort {
```

    // Function to merge the two sorted arrays

    static void merge(int[] array,int low,int mid,int high){

```
        int i,j,k;
```
```
        int[] c= new int[high-low+1];
```
```
        k = 0;
```
```
        i=low;
```
```
        j=mid+1;
```
```
        while(i<=mid && j<=high){
```
```
            if(array[i]<=array[j]){
```
```
                c[k++] = array[i++];
```
```
            }
```
```
            else{
```
```
                c[k++] = array[j++];
```
```
            }
```
```
        }
```
```
        while(i<=mid){
```
```
            c[k++] = array[i++];
```
```
        }
```
```
        while(j<=high){
```
```
            c[k++] = array[j++];
```
```
        }
```
```
        k=0;
```
```
        for(i = low; i<=high; i++){
```
```
            array[i] = c[k++];
```
```
        }
```
```
    }
```

    // Function implementing the merge sort

    static void mergeSort(int[] array,int low, int high){

```
        if(high-low+1>1){
```
```
            int mid = (low+high)/2;
```
```
            mergeSort(array,low,mid);
```

            mergeSort(array,mid+1,high);

```
            merge(array,low,mid,high);
```
```
        }
```
```
    }
```

    // Function to read the input and display the output

    public static void main(String[] args) {

        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

```
        int size;
```

        System.out.println("Enter the size of the array");

```
        try {
```

            size = Integer.parseInt(br.readLine());

```
        } catch (Exception e) {
```

            System.out.println("Invalid Input");

```
            return;
```
```
        }
```
```
        int[] array = new int[size];
```

        System.out.println("Enter array elements");

```
        int i;
```

        for (i = 0; i < array.length; i++) {

```
            try {
```

                array[i] = Integer.parseInt(br.readLine());

```
            } catch (Exception e) {
```

                System.out.println("An error Occurred");

```
            }
```
```
        }
```

        System.out.println("The initial array is");

        System.out.println(Arrays.toString(array));

        mergeSort(array,0,array.length-1);

        System.out.println("The sorted array is");

        System.out.println(Arrays.toString(array));

```
    }
```
```
}
```

Program Explanation

1. In function mergeSort(), first, we check if there is more than one element in the array, through the condition if(high-low+1>1).
2. If that is the case, a recursive call is made on the two halves obtained by dividing the array.
3. In function merge(), the while(i<=mid && j<=high) loop merges the elements of the two array into the new array c.
4. The loops while(i<=mid) and while(j<=high), adds any remaining elements of the arrays, at the end of c.

Note: Join free Sanfoundry classes at Telegram or Youtube

Time Complexity: O(n*log(n))
Time Complexity of Merge Sort is O(nlogn) for best, average, and worst case. Where n is the number of elements in the array.

Space Complexity: O(n)
Space Complexity of Merge Sort using an array is O(n), because Merge Sort requires an Auxiliary/temporary array for copying the elements.

Runtime Test Cases

Test Case 1: Here, the elements are reverse sorted.

 
Enter the size of the array
5
Enter array elements
5
4
3
2
1
The initial array is
[5, 4, 3, 2, 1]
The sorted array is
[1, 2, 3, 4, 5]

Test Case 2: Here, the elements are entered in random order.

 
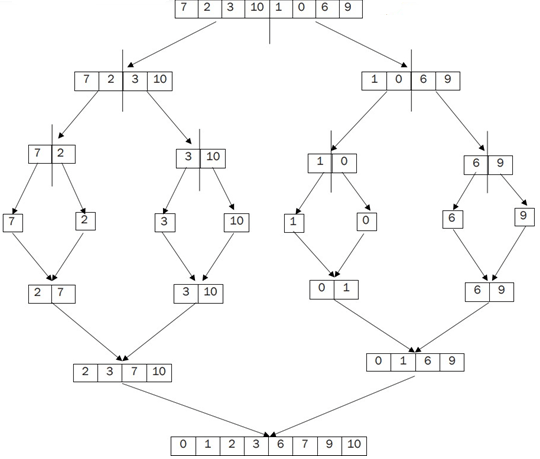
Enter the size of the array
8
Enter array elements
7
2
3
10
1
0
6
9
The initial array is
[7, 2, 3, 10, 1, 0, 6, 9]
The sorted array is
[0, 1, 2, 3, 6, 7, 9, 10]

Advantages of Merge Sort Algorithm:

Merge sort is an efficient sorting algorithm in Java, with an average and worst-case time complexity of O(n log n).
Merge sort has a simple and elegant recursive implementation, making it easy to understand and implement in Java.
Merge sort uses the divide and conquer technique, which reduces the problem into smaller subproblems until they can be solved directly.
Merge sort has a space complexity of O(n), making it suitable for sorting large datasets without running out of memory.
Merge sort is a stable sorting algorithm, which preserves the relative order of equal elements in the input array.
Merge sort is suitable for sorting complex data structures such as arrays of objects or strings.

Drawbacks:

For Small datasets merge sort is slower than other algorithms such as selection or insertion sort.
It requires additional space of O(n).
Even if the array is sorted Merge Sort will run completely.

To practice programs on every topic in Java, please visit “Programming Examples in Java”, “Data Structures in Java” and “Algorithms in Java”.

« Prev - Java Program to Implement Insertion Sort

» Next - Java Program to Implement Heap Sort

Related Posts:

Recommended Articles: