This set of Heat Transfer Multiple Choice Questions & Answers (MCQs) focuses on “Planck’s Law”.
1. The energy emitted by a black surface should not vary in accordance with
a) Wavelength
b) Temperature
c) Surface characteristics
d) Time
View Answer
Explanation: It is time independent. For a prescribed wavelength, the body radiates much more energy at elevated temperatures.
2. In the given diagram let r be the length of the line of propagation between the radiating and the incident surfaces. What is the value of solid angle W?
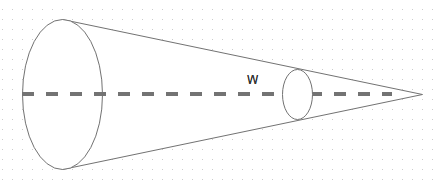
a) A sin α
b) A cos α
c) 2A cos α
d) 2A cos α
View Answer
Explanation: The solid angle is defined by a region by the rays of a sphere, and is measured as A n/r2.
3. Likewise the amount of emitted radiation is strongly influenced by the wavelength even if temperature of the body is
a) Constant
b) Increasing
c) Decreasing
d) It is not related with temperature
View Answer
Explanation: Temperature must remain constant in order to emit radiation.
4. A small body has a total emissive power of 4.5 kW/m2. Determine the wavelength of emission maximum
a) 8.46 micron m
b) 7.46 micron m
c) 6.46 micron m
d) 5.46 micron m
View Answer
Explanation: (Wavelength) max t = 2.8908 * 10 -3.
5. The sun emits maximum radiation of 0.52 micron meter. Assuming the sun to be a black body, Calculate the emissive ability of the sun’s surface at that temperature
a) 3.47 * 10 7 W/m2
b) 4.47 * 10 7 W/m2
c) 5.47 * 10 7 W/m2
d) 6.47 * 10 7 W/m2
View Answer
Explanation: E = σ b t 4 = 5.47 * 10 7 W/m2.
6. The law governing the distribution of radiant energy over wavelength for a black body at fixed temperature is referred to as
a) Kirchhoff’s law
b) Planck’s law
c) Wein’s formula
d) Lambert’s law
View Answer
Explanation: This law gives a relation between energy over wavelength.
7. The Planck’s constant h has the dimensions equal to
a) M L 2 T -1
b) M L T -1
c) M L T -2
d) M L T
View Answer
Explanation: It has unit equal to J s and its value is 6.626 * 10 -34.
8. Planck’s law is given by
a) (E) b = 2 π c 2 h (Wavelength) -5/[c h/k (Wavelength) T] – 2
b) (E) b = π c 2 h [exponential [c h/k (Wavelength) T] – 3].
c) (E) b = 2 π c 2 h (Wavelength) -5/exponential [c h/k (Wavelength) T] – 1
d) (E) b = 2 c 2 h (Wavelength) -5/exponential [c h/k (Wavelength) T] – 6
View Answer
Explanation: Planck suggested the following law for the spectral distribution of emissive power.
9. A furnace emits radiation at 2000 K. Treating it as a black body radiation, calculate the monochromatic radiant flux density at 1 micron m wavelength
a) 5.81 * 10 7 W/m2
b) 4.81 * 10 7 W/m2
c) 3.81 * 10 7 W/m2
d) 2.81 * 10 7 W/m2
View Answer
Explanation: (E) b = C 1 (Wavelength) -5/exponential [C 2/ (Wavelength) T] – 1.
10. A metal sphere of surface area 0.0225 m2 is in an evacuated enclosure whose walls are held at a very low temperature. Electric current is passed through resistors embedded in the sphere causing electrical energy to be dissipated at the rate of 75 W. If the sphere surfaces temperature is measured to be 560 K, while in steady state, calculate emissivity of the sphere surface
a) 0.498
b) 0.598
c) 0.698
d) 0.798
View Answer
Explanation: E = e A σ b T.
Sanfoundry Global Education & Learning Series – Heat Transfer.
To practice all areas of Heat Transfer, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Heat Transfer Books
- Apply for Chemical Engineering Internship
- Check Chemical Engineering Books
- Practice Mechanical Engineering MCQs
- Apply for Mechanical Engineering Internship
