Heat Transfer Questions and Answers – Effect of Variable Conductivity

This set of Heat Transfer Multiple Choice Questions & Answers (MCQs) focuses on “Effect Of Variable Conductivity”.

1. With variable thermal conductivity, Fourier law of heat conduction through a plane wall can be expressed as
a) Q = -k₀ (1 + β t) A d t/d x
b) Q = k₀ (1 + β t) A d t/d x
c) Q = – (1 + β t) A d t/d x
d) Q = (1 + β t) A d t/d x
View Answer

2. The inner and outer surfaces of a furnace wall, 25 cm thick, are at 300 degree Celsius and 30 degree Celsius. Here thermal conductivity is given by the relation
K = (1.45 + 0.5 * 10^-5 t²) KJ/m hr deg
Where, t is the temperature in degree centigrade. Calculate the heat loss per square meter of the wall surface area?
a) 1355.3 kJ/m² hr
b) 2345.8 kJ/m² hr
c) 1745.8 kJ/m² hr
d) 7895.9 kJ/m² hr
View Answer

3. A plane wall of thickness δ has its surfaces maintained at temperatures T₁ and T₂. The wall is made of a material whose thermal conductivity varies with temperature according to the relation k = k₀ T². Find the expression to work out the steady state heat conduction through the wall?
a) Q = 2A k₀ (T ₁ ³ – T ₂ ³)/3 δ
b) Q = A k₀ (T ₁ ³ – T ₂ ³)/3 δ
c) Q = A k₀ (T ₁ ² – T ₂ ²)/3 δ
d) Q = A k₀ (T ₁ – T ₂)/3 δ
View Answer

4. The mean thermal conductivity evaluated at the arithmetic mean temperature is represented by
a) k_m = k₀ [1 + β (t₁ – t₂)/2].
b) k_m = k₀ [1 + (t₁ + t₂)/2].
c) k_m = k₀ [1 + β (t₁ + t₂)/3].
d) k_m = k₀ [1 + β (t₁ + t₂)/2].
View Answer

5. With respect to the equation k = k₀ (1 +β t) which is true if we put β = 0?
a) Slope of temperature curve is constant
b) Slope of temperature curve does not change
c) Slope of temperature curve increases
d) Slope of temperature curve is decreases
View Answer

6. The accompanying sketch shows the schematic arrangement for measuring the thermal conductivity by the guarded hot plate method. Two similar 1 cm thick specimens receive heat from a 6.5 cm by 6.5 cm guard heater. When the power dissipation by the wattmeter was 15 W, the thermocouples inserted at the hot and cold surfaces indicated temperatures as 325 K and 300 K. What is the thermal conductivity of the test specimen material?

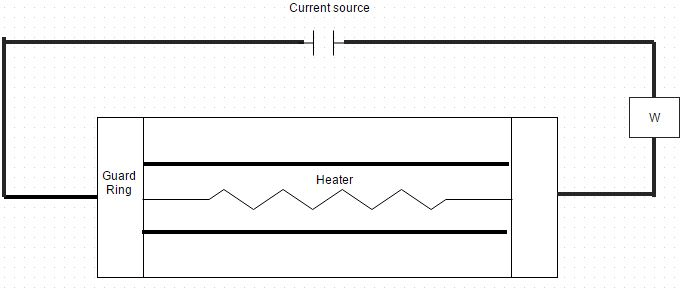
a) 0.81 W/m K
b) 0.71 W/m k
c) 0.61 W/m K
d) 0.51 W/m K
View Answer

7. If β is greater than zero, then choose the correct statement with respect to given relation
k = k₀ (1 +β t)
a) k doesn’t depend on temperature
b) k depends on temperature
c) k is directly proportional to t
d) Data is insufficient
View Answer

8. The unit of thermal conductivity doesn’t contain which parameter?
a) Watt
b) Pascal
c) Meter
d) Kelvin
View Answer

9. The temperatures on the two sides of a plane wall are t₁ and t₂ and thermal conductivity of the wall material is prescribed by the relation
K = k₀ e ^(-x/δ)
Where, k₀ is constant and δ is the wall thickness. Find the relation for temperature distribution in the wall?
a) t ₁ – t _x / t ₁ – t ₂ = x
b) t ₁ – t _x / t ₁ – t ₂ = δ
c) t ₁ – t _x / t ₁ – t ₂ = δ/x
d) t ₁ – t _x / t ₁ – t ₂ = x/δ
View Answer

10. “If β is less than zero, then with respect to the relation k = k₀ (1 + β t), conductivity depends on surface area”.
a) True
b) False
View Answer

Sanfoundry Global Education & Learning Series – Heat Transfer.

To practice all areas of Heat Transfer, here is complete set of 1000+ Multiple Choice Questions and Answers.

If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]