This set of Heat Transfer Multiple Choice Questions & Answers (MCQs) focuses on “Conduction Through A Sphere”.
1. The temperature distribution associated with radial conduction through a sphere is represented by
a) Parabola
b) Hyperbola
c) Linear
d) Ellipse
View Answer
Explanation: As conduction is radial i.e. in outward direction, so it follows the hyperbola equation..
2. The thermal resistance for heat conduction through a spherical wall is
a) (r2-r1)/2πkr1r2
b) (r2-r1)/3πkr1r2
c) (r2-r1)/πkr1r2
d) (r2-r1)/4πkr1r2
View Answer
Explanation: We get this on integrating the equation Q = -k A d t/ d r from limits r1 to r2 and T1 to T2.
3. The rate of conduction heat flow in case of a composite sphere is given by
a) Q = t1 – t2/ (r2 – r1)/4πk1r1r2 + (r3 – r2 )/4πk2r2r3
b) Q = t1 – t2/ (r2 – r1)/4πk1r1r2 + (r3 – r2 )/4πk2r2r3
c) Q = t1 – t2/ (r2 – r1)/4πk1r1r2 + (r3 – r2 )/4πk2r2r3
d) Q = t1 – t2/ (r2 – r1)/4πk1r1r2 + (r3 – r2 )/4πk2r2r3
View Answer
Explanation: Here, convective film coefficient at the inner and outer surfaces are also considered.
4. The thermal resistance for heat conduction through a hollow sphere of inner radius r1 and outer radius r2 is
a) r 2 – r 1/4πk r 1r 2
b) r 2 /4πk r 1r 2
c) r 1/4πk r 1r 2
d) 4πk r 1r 2
View Answer
Explanation: As Q = d t/ R T. Here R T is thermal resistance.
5. A spherical vessel of 0.5 m outside diameter is insulated with 0.2 m thickness of insulation of thermal conductivity 0.04 W/m degree. The surface temperature of the vessel is – 195 degree Celsius and outside air is at 10 degree Celsius. Determine heat flow per m2 based on inside area
a) – 63.79 W/m2
b) – 73.79 W/m2
c) – 83.79 W/m2
d) – 93.79 W/m2
View Answer
Explanation: Heat flow based on inside area = Q/4 π r 2 = – 73.79 W/m2.
6. The quantity d t/Q for conduction of heat through a body i.e. spherical in shape is
a) ln (r2/r1)/2πLk
b) ln (r2/r1)/πLk
c) ln (r2/r1)/2Lk
d) ln (r2/r1)/2πk
View Answer
Explanation: We get this on integrating the equation Q = -k A d t/ d r from limits r1 to r2 and T1 to T2.
7. A spherical vessel of 0.5 m outside diameter is insulated with 0.2 m thickness of insulation of thermal conductivity 0.04 W/m degree. The surface temperature of the vessel is – 195 degree Celsius and outside air is at 10 degree Celsius. Determine heat flow
a) – 47.93 W
b) – 57.93 W
c) – 67.93 W
d) – 77.93 W
View Answer
Explanation: Q = 4 π k r 1 r 2 (t 1 – t 2)/r 2 – r 1 = -57.93 W.
8. If we increase the thickness of insulation of a circular rod, heat loss to surrounding due to
a) Convection and conduction increases
b) Convection and conduction decreases
c) Convection decreases while that due to conduction increases
d) Convection increases while that due to conduction decreases
View Answer
Explanation: In convection energy is transferred between solid and fluid but in conduction from T 1 to T 2.
9. The following data pertains to a hollow cylinder and a hollow sphere made of same material and having the same temperature drop over the wall thickness
Inside radius = 0.1 m and outside surface area = 1 square meter
If the outside radius for both the geometrics is same, calculate the ratio of heat flow in the cylinder to that of sphere?
a) 0.056
b) 2.345
c) 1.756
d) 3.543
View Answer
Explanation: For sphere r 2 = (1/4 π) 1/2 = 0.282 m, for cylinder, l = A 2/2 r 2 π = 0.565 m.
10. The oven of an electric store, of total outside surface area 2.9 m2 dissipates electric energy at the rate of 600 W. The surrounding room air is at 20 degree Celsius and the surface coefficient of heat transfer between the room air and the surface of the oven is estimated to be 11.35 W/m 2 degree. Determine the average steady state temperature of the outside surface of the store
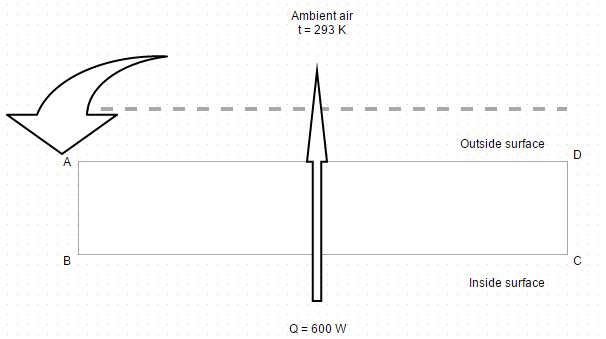
a) 38.22 degree Celsius
b) 48.22 degree Celsius
c) 58.22 degree Celsius
d) 68.22 degree Celsius
View Answer
Explanation: Q = h A (t 0 – t a).
Sanfoundry Global Education & Learning Series – Heat Transfer.
To practice all areas of Heat Transfer, here is complete set of 1000+ Multiple Choice Questions and Answers.
