This set of Heat Transfer Multiple Choice Questions & Answers (MCQs) focuses on “Conduction Through A Cylindrical Wall”.
1. Typical examples of heat conduction through cylindrical tubes are not found in
a) Power plants
b) Oil refineries
c) Most process industries
d) Aircrafts
View Answer
Explanation: Boilers have tubes in them, the condenser consist of a bank of tubes.
2. The rate of heat conduction through a cylindrical tube is usually expressed as
a) Per unit length
b) Per unit area
c) Only length
d) Only area
View Answer
Explanation: It is expressed as per unit length rather than per unit area as done for plane walls.
3. A steel pipe of 20 mm inner diameter and 2 mm thickness is covered with 20 mm thick of fiber glass insulation (k = 0.05 W/m degree). If the inside and outside convective coefficients are 10 W/m2 degree and 5 W/m2 degree, calculate the overall heat transfer coefficient based on inside diameter of pipe. In the diagram, the diameter of small circle is 20 mm
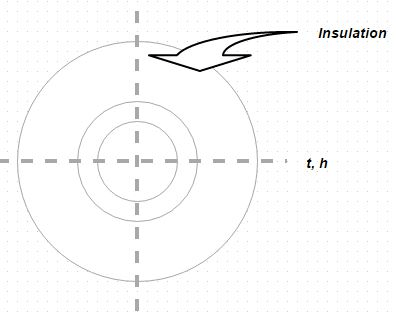
a) 1.789 W/m2 degree
b) 2.789 W/m2 degree
c) 3.789 W/m2 degree
d) 4.789 W/m2 degree
View Answer
Explanation: Q = 2 π l (t i – t 0)/ [(1/h i r i) + log e (r 3/r 2) (1/k 2) + (1/h 0 r 3)].
4. Logarithmic mean area of the cylindrical tube is given as
a) 2πr m
b) πr ml
c) 2πr ml
d) 2r ml
View Answer
Explanation: It is known as equivalent area and r m = r2-r1/log e (r2/r1).
5. A hot fluid is being conveyed through a long pipe of 4 cm outer diameter and covered with 2 cm thick insulation. It is proposed to reduce the conduction heat loss to the surroundings to one-third of the present rate by further covering with same insulation. Calculate the additional thickness of insulation
a) 11 cm
b) 12 cm
c) 13 cm
d) 14 cm
View Answer
Explanation: Heat loss with existing insulation = 2 π k l (t 1 – t 2)/log e (r 2/r 1) and heat loss with additional insulation = 2 π k l (t 1 – t 2)/log e (r 2 + x/r 1).
6. The heat flow equation through a cylinder of inner radius r1 and outer radius r2 is desired to be written in the same form as that for heat flow through a plane wall. For wall thickness (r2 – r1) the area will be
a) (A1 + A2)/2
b) (A1 + A2)
c) (A2 – A1)/(loge(A2/A1))
d) (A1 + A2)/(2 loge(A2/A1))
View Answer
Explanation: Here A 1 and A 2 are the inner and outer surface areas of tubes. The net area is AM.
7. A cylinder of radius r and made of material of thermal conductivity k 1 is surrounded by a cylindrical shell of inner radius r and outer radius 2r. This outer shell is made of a material of thermal conductivity k 2. Net conductivity would be
a) k 1 + 3 k 2/4
b) k 1 + k 2/4
c) k 1 + 3k 2
d) k 1 + k 2
View Answer
Explanation: Heat flowing per second is given by = k1 (πr2) (t1-t2) δ. Shell heat is k2 π [(2r)2 – r2 ] (t1 – t2)/ δ.
8. For steady state and a constant value of thermal conductivity, the temperature distribution associated with radial convection through a cylinder is
a) Linear
b) Parabolic
c) Logarithmic
d) Exponential
View Answer
Explanation: As thermal conductivity is constant so we get a profile that is logarithmic in nature.
9. A cylindrical cement tube of radii 0.05 cm and 1.0 cm has a wire embedded into it along its axis. To maintain a steady temperature difference of 120 degree Celsius between the inner and outer surfaces, a current of 5 ampere is made to flow in the wire. Find the amount of heat generated per meter length. Take resistance of wire equal to 0.1 ohm per cm of length
a) 150 W/m length
b) 250 W/m length
c) 350 W/m length
d) 450 W/m length
View Answer
Explanation: Resistance of wire = 10 ohm per m length. Heat generated = (5) 2 10 = 250 W/m length.
10. A stainless steel tube with inner diameter 12 mm, thickness 0.2 mm and length 50n cm is heated electrically. The entire 15 k W of heat energy generated in the tube is transferred through its outer surface. Find the intensity of the current flow
a) 52 amps
b) 62 amps
c) 72 amps
d) 82 amps
View Answer
Explanation: Power generated = 15 k W = 15000 W. Therefore, intensity of current flow = (15000/5.548) ½ = 52 amps.
Sanfoundry Global Education & Learning Series – Heat Transfer.
To practice all areas of Heat Transfer, here is complete set of 1000+ Multiple Choice Questions and Answers.
- Apply for Mechanical Engineering Internship
- Practice Mechanical Engineering MCQs
- Apply for Chemical Engineering Internship
- Check Heat Transfer Books
- Check Chemical Engineering Books
