This set of Heat Transfer Operations Interview Questions and Answers focuses on “HT Equipment – Combined Heat Transfer by Conduction and Convection”.
1. In a Heat Exchanger, heat cannot be transferred by all the three means, that is Conduction, Convection and Radiation simultaneously.
a) True
b) False
View Answer
Explanation: In a Heat Exchanger there can be maximum two possible means of heat transfer in practical use, they are Conduction and Convection.
2. Which is the correct temperature regime for combined Conduction and Natural Convection through a conducting wall?
a) 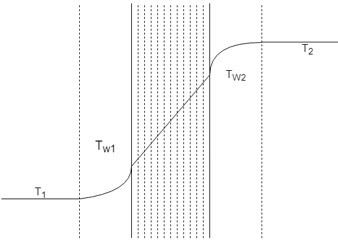
b) 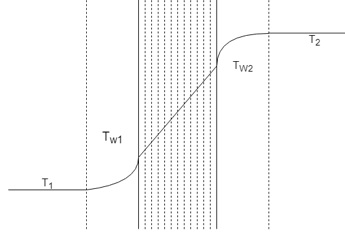
c) 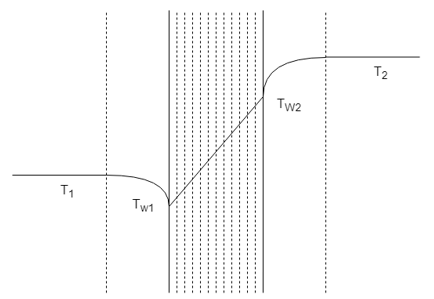
d) 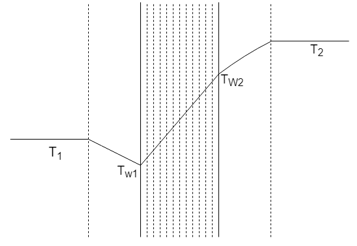
View Answer
Explanation: In the given plot, we can observe the temperature is uniform in both the bulk of the components in either side. The temperature profile in Conduction is always linear but parabolic at points very close to the wall surface.
3. In which one of the following, Heat transfer takes place without any Conduction or Convection?
a) Condenser
b) Recuperators
c) Cooling tower
d) Shell and Tube HE
View Answer
Explanation: In a cooling tower, heat transfer takes place by evaporation which carries away the thermal energy from the liquid in the form of vapour hence cooling it, no instance of conduction or convection is observed.
4. How many Heat Exchangers can be classified on the basis of phase change of the fluids?
a) 1
b) 2
c) 3
d) 4
View Answer
Explanation: For a heat exchanger to be classified on the basis of phase change of participating fluids, they can be classified into Condensers and Evaporators.
5. When we want to heat a stream of liquid by Steam, and the steam may condense into liquid. Then which of the following is best suited?
a) Steam on the side with the fins
b) Steam on the side with the fins and condensate drainage
c) Steam on the side with the fins and a brush to remove the condensate film from surface
d) Steam on the tube with the fins on inner surface of the tube passing through a pool of cooling liquid
View Answer
Explanation: As we know that film condensing is less effective than drop-wise condensing, hence a brush continuously removing the film is the best suit for this purpose.
6. Which one of the following relations are correct?
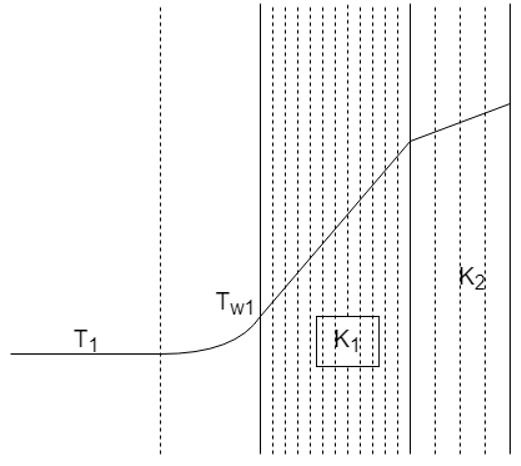
a) K1 < K2
b) K1 = K2
c) K1 > K2
d) K1 and K2 relation not defined
View Answer
Explanation: The more the conductivity, less is the resistivity to the heat flow, less is the slope of the temperature curve. Hence from the figure as slope of medium 1 is greater than medium 2, its conductivities are in opposite order, i.e. K1 < K2.
7. When we want to heat a stream of liquid by Steam, we usually keep removing the condensate from the surface of the tube.
a) True
b) False
View Answer
Explanation: It is best suited when we keep removing condensate from the tube surface as film condensation decreases the heat transfer coefficient and removing it supports drop-wise condensation.
8. What is the resistance of the following wall setup?
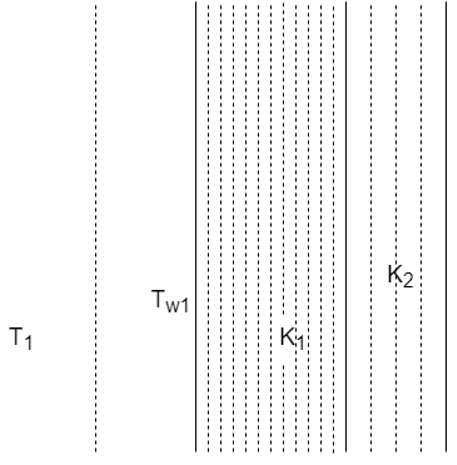
a) R = \(\frac{1}{h_1A}+\frac{L}{K_1}+\frac{1}{K_2}\)
b) R = \(\frac{1}{h_1A}+\frac{L}{K_1}+\frac{L}{K_2}\)
c) R = \(\frac{L}{h_1A}+\frac{L}{K_1}+\frac{L}{K_2}\)
d) R = \(\frac{1}{h_1A}+\frac{L}{K_1}+\frac{1}{h_1A}\)
View Answer
Explanation: The medium of T1 is a gas medium with its convective heat transfer coefficient as h1 and other two wall mediums are conductive with conductive heat transfer coefficient as K1 and K2 respectively hence the individual resistances combined is R = R1 + R2 + R3.
R = \(\frac{1}{h_1A}\) R = \(\frac{L}{K_1}\) R = \(\frac{L}{K_2}\).
9. What is the critical radius of insulation for a cylindrical wall?
a) \(\frac{K}{H}\)
b) \(\frac{4K}{H}\)
c) \(\frac{K}{4H}\)
d) \(\frac{H}{K}\)
View Answer
Explanation: The critical thickness of insulation is that radius of the insulating wall (with conductive heat transfer coefficient as K and the surrounding fluid convective heat transfer coefficient as H) that gives maximum heat transfer rate Q. Hence for a cylindrical insulating wall it is \(\frac{K}{H}\).
10. What is Critical radius of insulation?
a) The maximum radius that can allow heat transfer
b) The maximum heat transfer coefficient at a maximum possible radius
c) The radius at which maximum heat transfer rate is observed
d) The minimum radius at which maximum heat transfer rate is observed
View Answer
Explanation: The critical thickness of insulation is that radius (neither maximum nor minimum) of the insulating wall with conductive heat transfer coefficient as K and the surrounding fluid convective heat transfer coefficient as H, that gives maximum heat transfer rate Q.
11. Recognize the correct heat transfer rate pattern for critical radius of insulation.
a) 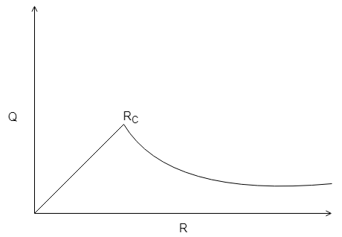
b) 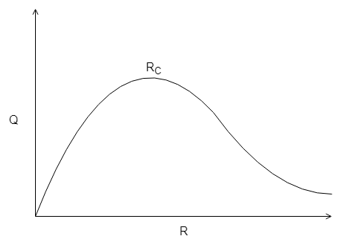
c) 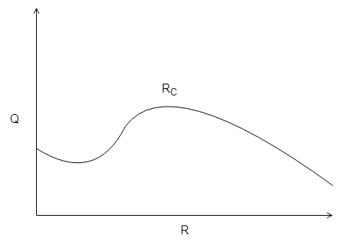
d) 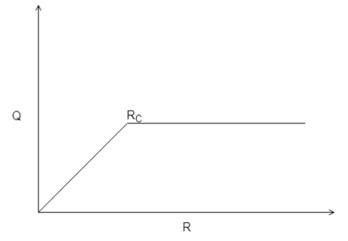
View Answer
Explanation: As the radius increases, the heat transfer rate also increases, but never linearly, then at a certain radius it reaches its maximum after which the heat transfer rate again decreases. Hence this point of inflection at that certain radius is called the critical radius of insulation (RC).
12. Which one of the following figures correctly shows the dotted line at the point of critical radius/ maximum heat transfer rate for a cylindrical tube wall?
a) 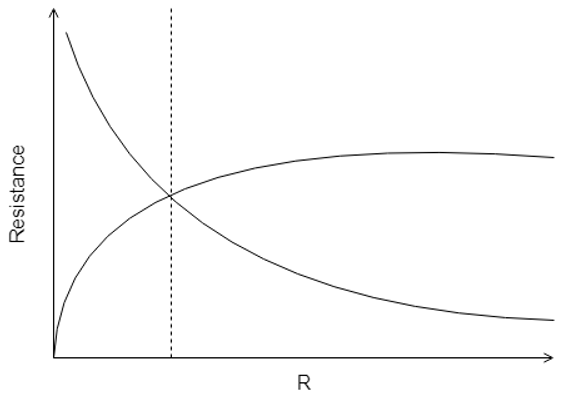
b) 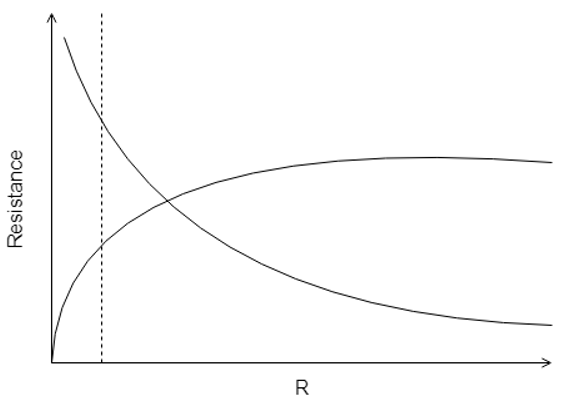
c) 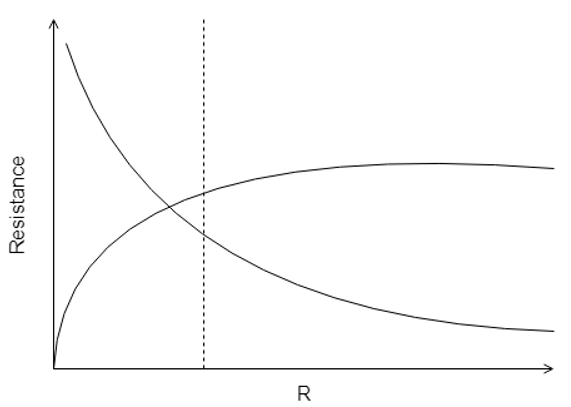
d) 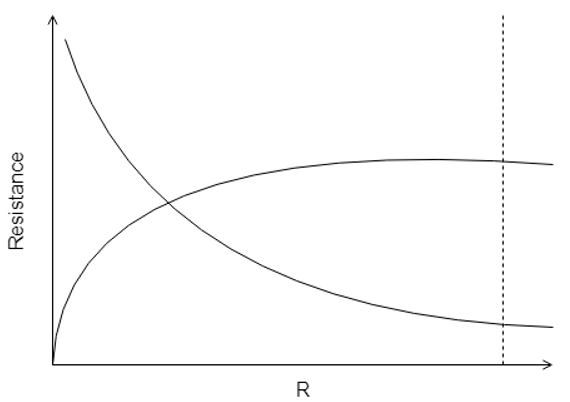
View Answer
Explanation: The critical thickness of insulation is that radius of the insulating wall with conductive heat transfer coefficient as K and the surrounding fluid convective heat transfer coefficient as H, that gives maximum heat transfer rate Q. The following figure will make it clear.
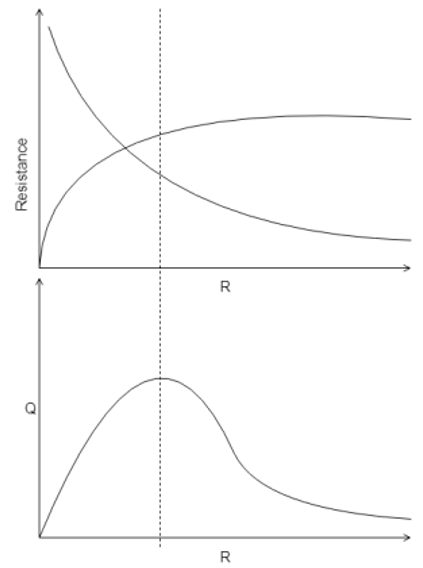
The dotted line denotes the critical radius of insulation.
13. What is critical thickness of insulation for a spherical insulator?
a) K⁄H
b) \(\frac{2K}{H}\)
c) \(\frac{4K}{H}\)
d) H⁄K
View Answer
Explanation: The critical thickness of insulation is that radius of the insulating wall (with conductive heat transfer coefficient as K and the surrounding fluid convective heat transfer coefficient as H) that gives maximum heat transfer Q. Hence for a spherical insulating wall it is \(\frac{2K}{H}\).
14. What is the expression for the rate of heat transfer for a cylindrical insulating wall covering a hot fluid?
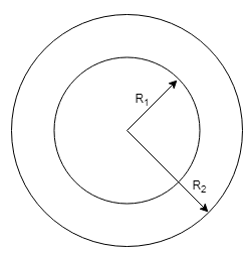
a) Q = \(\frac{2\pi(T-T_\infty)K}{\frac{K}{HR_2}+ln (\frac{R_2}{R_1})}\)
b) Q = \(\frac{2\pi(T_\infty-T)K}{\frac{K}{HR_1}+ln (\frac{R_2}{R_1})}\)
c) Q = \(\frac{2\pi(T-T_\infty)K}{\frac{K}{HR_2}+ln (\frac{R_1}{R_2})}\)
d) Q = \(\frac{2\pi(T_\infty-T)K}{\frac{K}{HR_2}+ln (\frac{R_2}{R_1})}\)
View Answer
Explanation: The total heat transfer rate can be defined as the net Temperature gradient to the total resistance of the medium. Hence the correct answer can also be represented as:
Q = \(\frac{(T-T_\infty)}{\frac{1}{2\pi HR_2}+\frac{ln(\frac{R_2}{R_1})}{2\pi K}} \)
15. For the calculation of critical radius of insulation for a cylindrical tube, which of the following differentiation is correct?
a) \(\frac{d(\frac{K}{HR_2}+ln(\frac{R_2}{R_1}))}{dR_1}\) = 0
b) \(\frac{d(\frac{K}{HR_1}+ln(\frac{R_2}{R_1}))}{dR_2}\) = 0
c) \(\frac{d(\frac{K}{HR_2}+ln(\frac{R_1}{R_2}))}{dR_1}\) = 0
d) \(\frac{d(\frac{K}{HR_2}+ln(\frac{R_2}{R_1}))}{dR_2}\) = 0
View Answer
Explanation: The total heat transfer rate can be defined as the net Temperature gradient to the total resistance of the medium. Hence the heat transfer rate can be represented as:
Q = \(\frac{2\pi(T-T_\infty)K}{\frac{K}{HR_2}+ln(\frac{R_2}{R_1})}\)
thus to calculate the maximum heat transfer rate at a given thickness, we differentiate the denominator to zero for the minimum of the denominator component which will fetch us the maximum heat transfer rate Q. We differentiate it with respect to R2 as it is the only variable with R1 a fixed constant.
Sanfoundry Global Education & Learning Series – Heat Transfer Operations.
To practice all areas of Heat Transfer Operations for Interviews, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Chemical Engineering Books
- Apply for Chemical Engineering Internship
- Check Heat Transfer Operations Books
- Practice Chemical Engineering MCQs
