This set of Electronic Devices and Circuits Multiple Choice Questions & Answers (MCQs) focuses on “Random Process”.
1. For random process X = 6 and Rxx (t, t+t) = 36 + 25 exp(|t|). Consider following statements:
(i) X(t) is first order stationary.
(ii) X(t) has total average power of 36 W.
(iii) X(t) is a wide sense stationary.
(iv) X(t) has a periodic component.
Which of the following is true?
a) i, ii, and iv
b) ii, iii, and iv
c) ii and iii
d) only iii
View Answer
Explanation: X Constant and Rxx() is not a function of t, so X(t) is a wide sense stationary. So (i) is false & (iii) is true. Pxx = Rxx(0) 36+25 = 61. Thus (ii) is false if X(t) has a periodic component, then RXX(t) will have a periodic component with the same period. Thus (iv) is false.
2. White noise with power density No/2 = 6 microW/Hz is applied to an ideal filter of gain 1 and bandwidth W rad/s. If the output’s average noise power is 15 watts, the bandwidth W is
a) 2.5 x 10 (-6)
b) 2.5p x 10 (-6)
c) 5 x 10 (-6)
d) p5 x 10 (-6)
View Answer
Explanation: Pyy = 1/2p Integral(?xx(w) |H(w)|^2 dw ) from plus infinity to minus infinity. Hence solve for W.
3. The two-level semi-random binary process is defined by X(t) A or -A where (n 1)T < t < nt and the levels A and -A occur with equal probability. T is a positive constant and n = 0, ±1, ±2. What is the mean value of E[X(t)]?
a) 1/2
b) 1/4
c) 1
d) 0
View Answer
Explanation: E[X(t)] = A P(A) – (-A)P(-A) which is zero.
4. The two-level semi-random binary process is defined by X(t) A or -A where (n 1)T < t < nt and the levels A and -A occur with equal probability. T is a positive constant and n = 0, ±1, ±2. Then the autocorrelation Rxx(t1 = 0.5T, t2 = 0.7T) will be?
a) 1
b) 0
c) A x A
d) 0.5 (A x A)
View Answer
Explanation: Here Rxx is AxA if both t1 and t2 are different and zero if they are same. Hence the answer is AxA.
5. Air craft of Jet Airways at Ahmedabad airport arrive according to a Poisson process at a rate of 12 per hour. All aircraft are handled by one air traffic controller. If the controller takes a 2 – minute coffee break, what is the probability that he will miss one or more arriving aircraft?
a) 0.33
b) 0.44
c) 0.55
d) 0.66
View Answer
Explanation: P (miss/or more aircraft) = 1 – P(miss 0) = 1 – P(0 arrive).
6. A stationary random process X(t) is applied to the input of a system for which h(t) = u(t) t2 e(-8t). If E[X(t)] = 2, the mean value of the system’s response Y(t) is
a) 1/128
b) 1/64
c) 3/128
d) 1/32
View Answer
Explanation: The mean value of Y(t) is integral of h(t)dt over negative infinity to positive infinity which gives the value equal to 3/128.
7. A random process is defined by X(t) + A where A is continuous random variable uniformly distributed on (0,1). The auto correlation function and mean of the process is
a) 1/2 & 1/3
b) 1/3 & 1/2
c) 1 & 1/2
d) 1/2 & 1
View Answer
Explanation: E[X(t)X(t+t)] = 1/3 and E[X(t)] = 1/2 respectively.
8. The auto correlation function of a stationary ergodic random process is shown below.
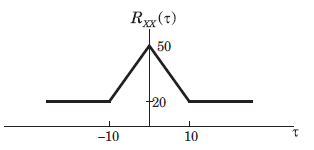
What is the mean value E[X(t)]?
a) 50
b) sqrt(50)
c) 20
d) sqrt(20)
View Answer
Explanation: Lim |t| tends to infinity, Rxx(t) = 20 = X2. hence X is sqrt(20).
9. The auto correlation function of a stationary ergodic random process is shown below.

What is E[X2(t)]?
a) 10
b) sqrt(10)
c) 50
d) sqrt(50)
View Answer
Explanation: Rxx(0) = X2 = 50.
10. The auto correlation function of a stationary ergodic random process is shown below.

What is the value of variance?
a) 20
b) 50
c) 70
d) 30
View Answer
Explanation: Here X = 0, y = 0, Rxx(0) = 5, Ryy(0) = 10. The only value that satisfies all the given conditions is 30.
Sanfoundry Global Education & Learning Series – Electronic Devices and Circuits.
To practice all areas of Electronic Devices and Circuits, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
