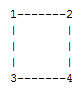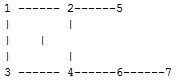Dominating Set Problem in C++

This is a C++ Program To Implement Heuristic To Find A Dominant Of A Given Graph.

The problem takes E edges as input and outputs Dominant Set of the graph, implementing the following heuristic.

Dominant Set of a Graph is to find, a set of vertices S, such that for every vertex in the graph, it is an adjacent vertex to atleast one of the vertex in the set S.

Example:

Possible Dominant Sets are: S = {1,3} or {1,2} or {1,4} and many more.

Example:

Some of the possible Dominant Sets are: {1,2,4,7} or {1,3,5,6} and many more.

There is no polynomial time algorithm invented up to date to find the minimum size Dominant Set, though many approximate algorithms(heuristics) do exist. Here, implementation of one such heuristic is shown. Size of Dominant, is the cardinality of the Dominant Set.

1. Initialize a set S as empty.
2. Take an edge E of the graph connecting lets say, A and B.
3. Add one vertex (let say A) to our set S.
4. Discard all edges in the graph with endpoints at A.
5. Go to step 2, if some edge is till left in the graph.
6. The final set S is a Dominant Set of the graph.

Here is source code of the C++ Program to generate Dominant Set for a given graph. The program is successfully compiled and tested under Linux platform. The program output is also shown below.

#include<bits/stdc++.h>
 
using namespace std;
 
vector<vector<int> > graph;
bool vis[100011];
int i,j;
 
vector<int> solve_dominant(int n,int e)
{
	vector<int> S;
	for(i=0;i<n;i++)
	{
		if(!vis[i])
		{
			S.push_back(i);
			vis[i]=true;
			for(j=0;j<(int)graph[i].size();j++)
			{
				if(!vis[graph[i][j]])
				{
					vis[graph[i][j]]=true;
					break;
				}
			}
		}
	}
	return S;
}
int main()
{
	int n,e,x,y;
	cout<<"Enter number of vertices:";
	cin>>n;
	cout<<"Enter number of Edges:";
	cin>>e;
	graph.resize(n);
	memset(vis,0,sizeof(vis));
	for(i=0;i<e;i++)
	{
		cout<<"Enter the end-points of edge "<<i+1<<" : ";
		cin>>x>>y;
		x--; y--;
		graph[x].push_back(y);
		graph[y].push_back(x);
	}
	vector<int> S = solve_dominant(n,e);
	cout<<"The required Dominant Set is as follows:\n";
	for(i=0;i<(int)S.size();i++)
	cout<<S[i]+1<<" ";
	return 0;
}

1. User must first enter the number of vertices, N, and then number of edges, E, in the graph.
2. It should be followed by E lines, denoting A and B, if there is an edge between A and B.
3. The graph is stored as adjacency list.
4. Then the Heuristic is implemented, with our vector “S” as the final vertex cover using “solve_dominant()” function.

 
Enter number of vertices:5
Enter number of Edges:6
Enter the end-points of edge 1 : 1 2
Enter the end-points of edge 2 : 2 3
Enter the end-points of edge 3 : 3 4
Enter the end-points of edge 4 : 1 4
Enter the end-points of edge 5 : 4 5
Enter the end-points of edge 6 : 3 5
The required Dominant Set is as follows:
1 3 5 
 
Case 2:
Enter number of vertices:4
Enter number of Edges:3
Enter the end-points of edge 1 : 1 2
Enter the end-points of edge 2 : 1 3
Enter the end-points of edge 3 : 3 4
The required Dominant Set is as follows:
1 3

Sanfoundry Global Education & Learning Series – C++ Algorithms.
To practice all C++ Algorithms, here is complete set of 1000 C++ Algorithms.