This set of Control Systems Multiple Choice Questions & Answers (MCQs) focuses on “Time Response of Second Order Systems – I”.
1. Which of the following transfer function will have the greatest maximum overshoot?
a) 9/(s2+2s+9)
b) 16/(s2+2s+16)
c) 25/(s2+2s+25)
d) 36/(s2+2s+36)
View Answer
Explanation: Comparing the characteristic equation with the standard equation the value of the damping factor is calculated and the value for the option d is minimum hence the system will have the maximum overshoot .
2. A system generated by ![]() The ramp component in the forced response will be:
The ramp component in the forced response will be:
a) t u(t)
b) 2t u(t)
c) 3t u(t)
d) 4t u(t)
View Answer
Explanation:
Laplace transforming
sY(s) + 2Y(s)=4/s2
Taking the inverse Laplace transform the forced term is 2t u(t).
3. The system in originally critically damped if the gain is doubled the system will be :
a) Remains same
b) Overdamped
c) Under damped
d) Undamped
View Answer
Explanation:
From question g1 = 1, k1 = x ,k2 = 2x then we need to find g2 .
By substituting all these values the g2 values would lies between 0 and 1.
4. Let c(t) be the unit step response of a system with transfer function K(s+a)/(s+K). If c(0+) = 2 and c(∞) = 10, then the values of a and K are respectively.
a) 2 and 10
b) -2 and 10
c) 10 and 2
d) 2 and -10
View Answer
Explanation: Applying initial value theorem which state that the initial value of the system is at time t =0 and this is used to find the value of K and final value theorem to find the value of a.
5. The damping ratio and peak overshoot are measures of:
a) Relative stability
b) Speed of response
c) Steady state error
d) Absolute stability
View Answer
Explanation: Speed of response is the speed at which the response takes the final value and this is determined by damping factor which reduces the oscillations and peak overshoot as the peak is less then the speed of response will be more.
6. Find the type and order of the system given below:
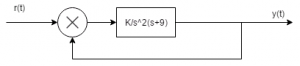
a) 2,3
b) 2,2
c) 3,3
d) None of the mentioned
View Answer
Explanation: Type = 2 which is the number of poles at the origin and order is the highest power of the characteristic equation.
7. A system has a complex conjugate root pair of multiplicity two or more in its characteristic equation. The impulse response of the system will be:
a) A sinusoidal oscillation which decays exponentially; the system is therefore stable
b) A sinusoidal oscillation with a time multiplier ; the system is therefore unstable
c) A sinusoidal oscillation which rises exponentially ; the system is therefore unstable
d) A dc term harmonic oscillation the system therefore becomes limiting stable
View Answer
Explanation: Poles are the roots of the denominator of the transfer function and on imaginary axis makes the system stable but multiple poles makes the system unstable.
8. The forward path transfer function is given by G(s) = 2/s(s+3). Obtain an expression for unit step response of the system.
a) 1+2e-t+e-2t
b) 1+e-t-2e-2t
c) 1-e-t+2e-2t
d) 1-2e-t+e+2t
View Answer
Explanation: C(s)/R(s) = s/(s2+3s+2)
C(s) = 1/s-2/s+1+1/s+2
c(t) = 1-2e-t+e+2t.
9. Find the initial and final values of the following function:
F(s) = 12(s+1)/s(s+2)^2(s+3)
a) 1,∞
b) 0,∞
c) ∞,1
d) 0,1
View Answer
Explanation: Using final and initial values theorem directly to find initial and final values but keeping in mind that final value theorem is applicable for stable systems only.
10. The step response of the system is c(t) = 10+8e-t-4/8e-2t . The gain in time constant form of transfer function will be:
a) -7
b) 7
c) 7.5
d) -7.5
View Answer
Explanation: Differentiating the equation and getting the impulse response and then taking the inverse Laplace transform and converting the form into time constant form we get K = -7.5.
Sanfoundry Global Education & Learning Series – Control Systems.
To practice all areas of Control Systems, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Electrical Engineering Books
- Apply for Electrical Engineering Internship
- Apply for Electronics & Communication Engineering Internship
- Check Control System Books
- Practice Electrical Engineering MCQs
