Control Systems Questions and Answers – State Variable Analysis – II

This set of Control Systems Multiple Choice Questions & Answers focuses on “State Variable Analysis – II”.

1. State variable analysis has several advantages overall transfer function as:
a) It is applicable for linear and non-linear and variant and time-invariant system
b) Analysis of MIMO system
c) It takes initial conditions of the system into account
d) All of the mentioned
View Answer

2. The minimum number of states require to describe the two degree differential equation:
a) 1
b) 2
c) 3
d) 4
View Answer

3. For a system with the transfer function H(s) = 3(s-2)/s³+4s²-2s+1 , the matrix A in the state space form is equal to:
a)
\(\begin{matrix}1 & 0 & 0\\
0 & 1 & 0\\
-1 & 2 & -4\\
\end{matrix}
\)
b)
\(\begin{matrix}
0 & 1 & 0\\
3 & -2 & 1\\
1 & -2 & 4
\end{matrix}
\)
c)
\(\begin{matrix}
0 & 1 & 0\\
0 & 0 & 1\\
-1 & 2 & -4
\end{matrix}
\)
d)
\(\begin{matrix}
1 & 0 & 0\\
0 & 1 & 0\\
-1 & -2 & -4
\end{matrix}
\)
View Answer

4. The transfer function Y(s)/U(s) of a system described by the state equations dx/dt=-2x+2u and y(t) = 0.5x is:
a) 0.5/(s-2)
b) 1/(s-2)
c) 0.5/(s+2)
d) 1/(s+2)
View Answer

5. A linear time invariant single input single output system has the state space model given by dx/dt=Fx+Gu, y=Hz, where . Here, x is the state vector, u is the input, and y is the output. The damping ratio of the system is:
a) 0.25
b) 0.5
c) 1
d) 2
View Answer

6. Given the matrix
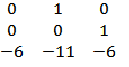the Eigen value are___________
a) 1,2,3
b) 1
c) -1,-2,-3
d) 0
View Answer

7. A transfer function of control system does not have pole-zero cancellation. Which one of the following statements is true?
a) System is neither controllable nor observable
b) System is completely controllable and observable
c) System is observable but uncontrollable
d) System is controllable but unobservable
View Answer

8. The analysis of multiple input multiple output is conveniently studied by;
a) State space analysis
b) Root locus approach
c) Characteristic equation approach
d) Nicholas chart
View Answer

9. The state equation in the phase canonical form can be obtained from the transfer function by:
a) Cascaded decomposition
b) Direct decomposition
c) Inverse decomposition
d) Parallel decomposition
View Answer

10. A logarithmic spiral extending out of the singular point is__________
a) Stable
b) Unstable focus
c) Conditionally stable
d) Marginally stable
View Answer

Sanfoundry Global Education & Learning Series – Control Systems.
To practice all areas of Control Systems, here is complete set of 1000+ Multiple Choice Questions and Answers.

If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]