This set of Civil Engineering Drawing Multiple Choice Questions & Answers (MCQs) focuses on “Loci of Points”.
1. The locus of a point P moving in a plane about another point O in such a way that its distance from it is constant, is called _________
a) Arc
b) Angle
c) Circle
d) Perpendicular bisector
View Answer
Explanation: According to locus postulate: The locus of a point P moving in a lane about another point in such a way that its distance from it is constant, is a circle of some radius.
2. The locus of a point equidistant from two fixed points A and B in the same plane, is the called ___________
a) Straight line
b) Angle
c) Circle
d) Perpendicular bisector
View Answer
Explanation: According to locus postulate: The locus of a point equidistant from two fixed points A and B in the same plane, is the perpendicular bisector of the line joining the two points.
3. The locus of a point equidistant from two fixed non-parallel straight line AB and CD is known as _______________
a) Straight line
b) Angular bisector
c) Circle
d) Perpendicular bisector
View Answer
Explanation: According to locus postulate: The locus of a point equidistant from two fixed non-parallel straight lines AB and CD will be a straight line bisecting the angle between them.
4. Using ruler and compass how will you construct ∆ABC, if AB=3.5, BC=6 and angle ABC=60o?
a) Draw line BC=6 cm and an angle CBA=600. Cut off AB=3.5. Join AC, triangle ABC is the required triangle
b) Draw line BC=6 cm and AB= 3.5 and then angle ABC=60o, ABC is the required triangle
c) Draw line AB= 3.5cm and cut off AB = 6 cm at any point and make angle CBA=600
d) Draw angle CBA= 600 and make
View Answer
Explanation: Figure below shows the construction:-
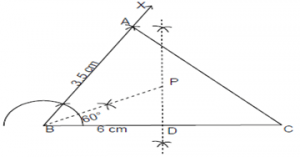
Draw line BC=6 cm with a ruler and an angle CBA=600 with the compass. Cut off AB=3.5 by compass. Join AC, triangle ABC is the required triangle.
5. Given 2 points A and B, what is the locus of points P so that angle APB is a right angle?
a) A square with points A and B
b) The circle with diameter AB
c) A rectangle with side A and B
d) A semi-circle with diameter AB
View Answer
Explanation: The circle with diameter AB, excluding points A and B will be the locus of point AB. This point P will always make 90° angle with the circumference when the lines from two points of radius meet at P, also from circle postulate it is proved.
6. For all value of the co-ordinates of a moving point Pare (a cos θ, b sin θ); what will be the equation to the locus of P?
a) x2/a2 + y2/b2 = 0
b) x2/b2 + y2/a2 = 0
c) x2/b2 + y2/a2 = 1
d) x2/a2 + y2/b2 = 1
View Answer
Explanation: Let (x, y) be the co-ordinates of any point on the locus traced out by the moving point P. Then we shall have
x = a cos θ or x/a = cos θ and y = b sin θ or, y/b = sin θ
x2/a2 + y2/b2 = cos2 θ + sin2 θ or, x2/a2 + y2/b2 = 1
which is the required equation to the locus of P.
7. What curve does the locus represent if the locus of a moving point which is always equidistant from the points (2, -1) and (3, 2)?
a) Hyperbola
b) Straight line
c) Ellipse
d) Circle
View Answer
Explanation: Let A (2, -1) and B (3, 2) be the given points and (x, y) be the co-ordinates of a point P on the required locus. Then,
PA2 = (x – 2)2 + (y + 1)2 and PB2 = (x – 3)2 + (y – 2)2
By problem, PA = PB or, PA2 = PB2
or, (x – 2)2 + (y + 1)2 = (x – 3)2 + (y – 2)2 or, x2 – 4x + 4 + y2 + 2y + 1 = x2 – 6x + 9 + y2 – 4y + 4
or, 2x + 6y = 8 or, x + 3y = 4 ……… (1)
Clearly, equation (1) is a first degree equation in x and y; hence, the locus of P is a straight line whose equation is x + 3y = 4.
8. A point moves in such a manner that three times of its abscissa is greater by 5 than two times of its ordinate; find the equation of its locus.
a) 3y-2y=5
b) 3x-2y=5
c) 2x+3y=5
d) 2x-3y=5
View Answer
Explanation: Here the terms abscissa and ordinate are the coordinates of a point in a two- dimensional rectangular Cartesian coordinate system where abscissa represents x-axis and ordinate as y-axis. So according to the given question the equation is as follows: 3x-2y=5.
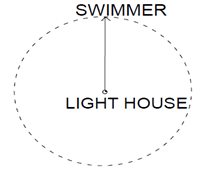
9. What will be the geometry made by a locus of a swimmer maintaining the same distant from the lighthouse?
a) Square
b) Rectangle
c) Circle
d) Triangle
View Answer
Explanation: The locus of the swimmer will be a circle with light house as the centre and the same distance between the light house and the swimmer as radius (locus postulate of a circle).
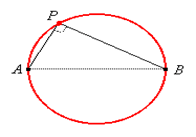
10. Which statement is correct for the locus shown in the figure below?
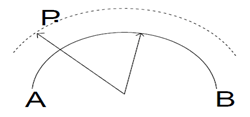
a) A point P moving in a plane about another point in such a way that its distance is constant
b) A point P moving in a plane about a fixed line as an arc with same centre
c) A point P moving in a plane about another point in such a way that its distance from a fixed line AB is constant
d) A point equidistant from two fixed non-parallel lines AB and CD in the same plane
View Answer
Explanation: As per arc postulate regarding locus it is stated as: When the fixed line is an arc of a circle, the locus will be another arc drawn through same centre. Here fixed line is an arc AB and the locus drawn is an arc representing the circumference, produced due to point P.
11. Four bar mechanism is generally used in ___________________
a) Bicycle
b) Fan
c) Train suspension
d) Rickshaw
View Answer
Explanation: Four-bar linkage, also called a four-bar, is the simplest movable closed chain linkage. It consists of four bodies, called bars or links, connected in a loop by four joints. Generally, the joints are configured so the links move in parallel planes, and the assembly is called a planar four-bar linkage.
12. Chords which are ___________ from the centre are equal.
a) unequal
b) equidistant
c) one third
d) two third
View Answer
Explanation: In the figure below, for ∆’s AOM and CON
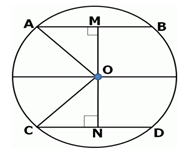
OM = ON (to prove)
OA = OC (radii of the same circle)
AM = CN OR 2AM = 2 CN (since OM ON are perpendicular to the chords and it bisects the chord and AM = MB, CN = ND)
Angle AMO and CNO = 90°
∆AOM similar to ∆CON (R.H.S rule)
OM = ON (CPCT) (required).
Sanfoundry Global Education & Learning Series – Civil Engineering Drawing.
To practice all areas of Civil Engineering Drawing, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Apply for Civil Engineering Internship
- Check Civil Engineering Drawing Books
- Check Civil Engineering Books
- Practice Civil Engineering MCQs