This set of Civil Engineering Drawing Multiple Choice Questions & Answers (MCQs) focuses on “Development of Surfaces”.
1. Which among these is not the method of surface development?
a) Parallel-line development
b) Radial-line development
c) Triangulation development
d) Geometric development
View Answer
Explanation: There is nothing like Geometric development. The surface development methods are-
Parallel-line Method: It is used for developing prisms and single curved surfaces like cylinders, in which all the edges/generation of lateral surfaces are parallel in each other.
Radial-line Method: It is employed for pyramids and single curved surfaces like cones in which the apex is taken as centre and the slant edge or generator as radius of its development.
Triangulation Method: It is used for developing transition pieces.
Approximate Method: It is employed for double curved surfaces like spheres, as they are theoretically not possible to develop. The surface of the sphere is developed by approximate method. When the surface is cut by a series of cutting planes, the cut surfaces is called a zone.
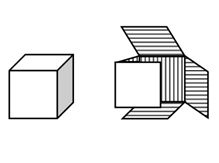
2. The shape of the development of the surface shown will be as a _______________
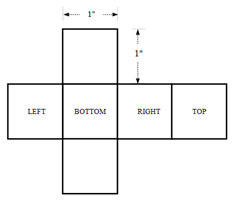
a) Cube
b) Cuboid
c) Triangular prism
d) Cone
View Answer
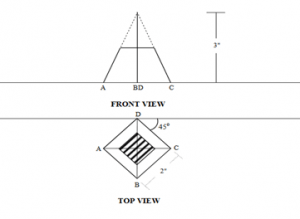
3. The front view obtained on the development of a square pyramid from its plan and front elevation which stands vertically on its base on H.P with one edge of the base parallel to V.P?
a) Square
b) Triangle
c) Trapezium
d) Rectangle
View Answer
4. The top view obtained by the development of a square pyramid from its plan and front elevation which stands vertically on its base on H.P with one edge of the base parallel to V.P. will be?
a) Triangle
b) Square
c) Trapezium
d) Circle
View Answer
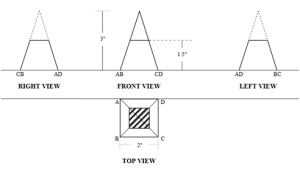
5. For a cone, the front view will be a ___________ with the slant edge showing the true length of the generator of the cone.
a) Square
b) Rectangle
c) Triangle
d) Circle
View Answer
6. Which method is used for development of a sphere?
a) Parallel-line development
b) Radial-line development
c) Triangulation development
d) Approximate method
View Answer
Explanation: Approximate Method: It is employed for double curved surfaces like spheres, as they are theoretically not possible to develop. The surface of the sphere is developed by approximate method. When the surface is cut by a series of cutting planes, the cut surfaces is called a zone.
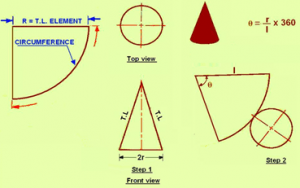
7. The development of cylinder is a _______
a) triangle
b) rectangle
c) square
d) trapezium
View Answer
Explanation:
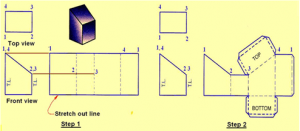
The figure above shows the development of a truncated rectangular prism.
Step 1: Draw the stretch-out line in the front view, along the base of the prism and equal in length to the perimeter of the prism.
Locate the fold lines on the pattern along the stretch-out line equal in length to the sides of the prism, 1-2, 2-3, 3-4, and 4-1.
Draw perpendicular construction lines at each of these points.
Project the points 1, 2, 3, and 4 from the front view
Step 2: Darken lines 1-2-3 and 4-1. Construct the bottom and top, as shown and add the seam to one end of the development and the top and bottom.
8. Zone method is used to develop _____________
a) prism
b) pyramid
c) cone
d) sphere
View Answer
Explanation: In this method the sphere is cut into a number of horizontal zones, each of which may be taken as frustum of a cone whose apex is at the extended chords. Now, develop each zone independently by radial line method. For example to develop the zone A, as it is a frustum of a rigid circular cone with its apex o, on the vertical axis of the sphere. Apply radial-line method and obtain the development of the zone.
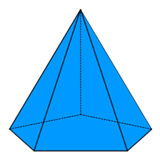
9. The development of lateral surfaces of a pentagonal pyramid is ________
a) Five rectangles
b) Five squares
c) Five triangles
d) Five circles
View Answer
Explanation: A pentagonal pyramid is a pyramid with a pentagonal base upon which are erected five triangular faces that meet at a point (the vertex). Like any pyramid, it is self-dual. The regular pentagonal pyramid has a base that is a regular pentagon and lateral faces that are equilateral triangles.
10. Rectangular prism is an example of __________
a) objects having isometric lines
b) object having non-isometric lines
c) object having curved surfaces
d) object having straight lines
View Answer
Explanation: Isometric lines – Designating a method of projection (isometric projection) in which a three-dimensional object is represented by a drawing (isometric drawing) having the horizontal edges of the object drawn usually at a 30° angle and all verticals projected perpendicularly from a horizontal base, all lines being drawn to scale.
11. The nature of surface of sphere is ______________
a) plane surface
b) singly curved surface
c) singly or doubly curved surface
d) doubly curved surface
View Answer
Explanation: Double-curved surfaces, such as a sphere do not produce true developments, because they do not contain any straight lines.
12. The method by which the development of surface of an oblique solid is obtained __________
a) radial line
b) parallel line
c) triangulation
d) approximation
View Answer
Explanation: In this method, the lateral surfaces of the transition pieces are divided in to a number of triangles. By finding the true lengths of the sides of each triangle, the development is drawn by laying each one of the triangles in their true shapes adjoining each other.
Sanfoundry Global Education & Learning Series – Civil Engineering Drawing.
To practice all areas of Civil Engineering Drawing, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Civil Engineering Drawing Books
- Practice Civil Engineering MCQs
- Apply for Civil Engineering Internship
- Check Civil Engineering Books