This set of Chemical Reaction Engineering Multiple Choice Questions & Answers (MCQs) focuses on “Reaction Kinetics Elements – Modelling the Rate Coefficient – 1”.
1. The value of rate constant for a zero order reaction is obtained by the plot between ____
a) Concentration vs time
b) Concentration vs rate
c) Rate vs time
d) Concentration vs rate
View Answer
Explanation: For a zero order reaction, \(\frac{-dC_A}{dt}\) = k
Integrating the above equation between initial concentration CA0 and final concentration CA, (CA0 – CA)=kt
The slope of the graph of concentration vs time gives the rate constant for a zero order reaction.
2. Which of the following theories does not propose the temperature dependence of rate constant?
a) Arrhenius theory
b) Collision theory
c) Transition state theory
d) Bohr’s theory
View Answer
Explanation: Bohr’s theory proposes the model of an atom. Arrhenius theory, Collision theory, Transition state theory propose the variation of rate constant with temperature.
3. Which among the following graphs represents a zero order reaction?
a)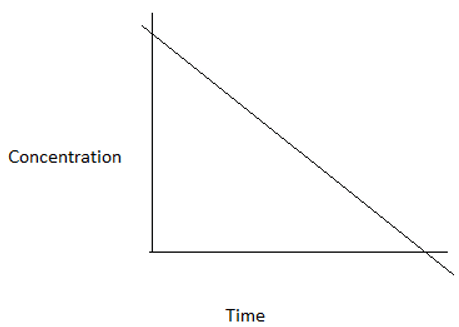 
b)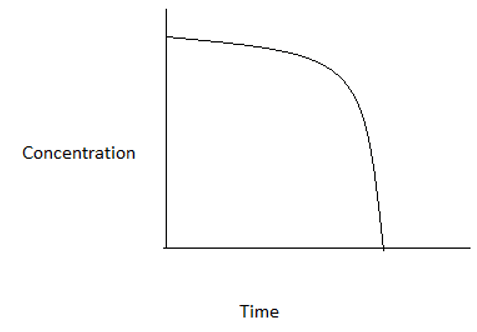 
c)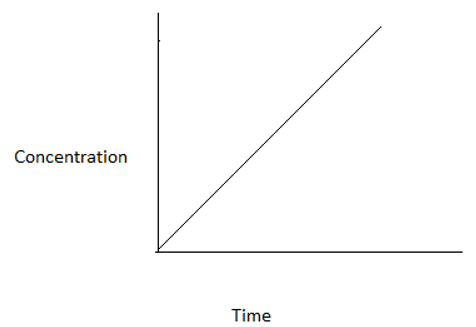 
d)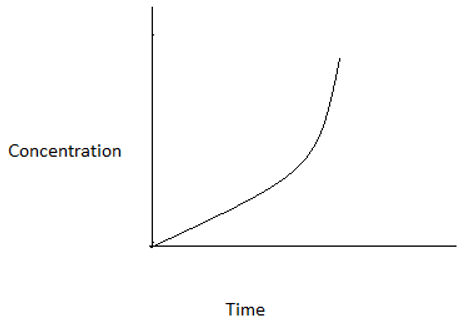 
View Answer
Explanation: For a zero order reaction, at time t=0, concentration=CA0. At time t=CA0/k, concentration=0. Hence, the graph is a straight line intercepting y- axis at CA0 and x- axis at CA0/k.
4. For a first order reaction, the rate constant as a function of half life is given as ____
a) \(\frac{0.6931}{k} \)
b) 0.6931×k
c) 0.6931
d) \(\frac{k}{0.6931} \)
View Answer
Explanation: Half life period is the time taken for one-half of the reactant to be consumed. For a first order reaction, (\(\frac{-dC}{dt}\)) = kCn. Integrating between initial concentration CA0 and final concentration \(\frac{C_{A0}}{2}\), ln(2) = kt0.5
t0.5 = \(\frac{0.6931}{k}.\)
5. The rate constant is a ____
a) Linear function of frequency factor
b) Exponential function of frequency factor
c) Logarithmic function of frequency factor
d) Sinusoidal function of frequency factor
View Answer
Explanation: By Arrhenius equation, k = \(Ae^{\frac{-E_a}{RT}}\)
K varies directly with respect to the frequency factor, A.
6. For any order n, the rate constant is expressed as ____
a) (-rA)
b) (-rA) × CAn
c) (-rA) × CA
d) \(\frac{-r_A}{C_A^n} \)
View Answer
Explanation: For any order n, (-rA) = kCAn. Hence, k = \(\frac{-r_A}{C_A^n}. \)
7. For a reaction with negative order n, which one of the following is true about reaction rate constant?
a) k = (-rA)
b) k = 1
c) k = \(\frac{-r_A}{C_A^n} \)
d) k = (-rA) × CAn
View Answer
Explanation: For n<0, (-rA) = kCAn
Hence, k = (-rA) × CAn
8. Which among the following is true for liquid phase reactions of order n?
a) ln(\(\frac{-dC}{dt}\)) = lnk + n(lnC)
b) ln(\(\frac{-dC}{dt}\)) = lnk + lnC
c) ln(\(\frac{-dC}{dt}\)) = nlnk + lnC
d) ln(\(\frac{-dC}{dt}\)) = lnk + \(\frac{lnC}{n} \)
View Answer
Explanation: (\(\frac{-dC}{dt}\)) = kCn
Taking natural logarithm on both sides, ln(\(\frac{-dC}{dt}\)) = lnk + n(lnC)
9. For a first order reaction, the rate constant is expressed in terms of initial concentration CAo and final concentration CA as ____
a) CA = CAo × k
b) CA = CAo × e-kt
c) CA = CAo × kt
d) CA = CAo × ekt
View Answer
Explanation: (\(\frac{-dC}{dt}\)) = kCA
ln(\(\frac{CAo}{CA}\)) = kt
CA = CAo × e-kt
10. If rate of a zero order reaction is 10 \(\frac{mol}{m^3×s}\) and reaction time is 5s, then the value of rate constant is ____
a) 1 s-1
b) 2 s-1
c) 5 s-1
d) 10 s-1
View Answer
Explanation: (-rA) = kCAn
10 = k (5)
Hence, k = 2 s-1.
Sanfoundry Global Education & Learning Series – Chemical Reaction Engineering.
To practice all areas of Chemical Reaction Engineering, here is complete set of 1000+ Multiple Choice Questions and Answers.
- Apply for Chemical Reaction Engineering Internship
- Practice Biotechnology MCQs
- Apply for Biotechnology Internship
- Buy Biotechnology Books
- Buy Chemical Engineering Books
