This set of Chemical Reaction Engineering Questions and Answers for Aptitude test focuses on “Rate Data Collection & Analysis – Method of Half Lives”.
1. State true or false.
For a second order reaction, t.0.5 is directly proportional to the initial concentration.
a) True
b) False
View Answer
Explanation: The general expression relating t.0.5, rate constant and initial concentration is t.0.5 = \(\frac{C_{A0}^{1-n}(2^{n-1}-1)}{(n-1)k}.\) For a second order reaction, t.0.5 = \(\frac{1}{kC_{A0}}.\) Hence, t.0.5 is inversely proportional to the initial concentration.
2. In terms of conversion, half life is the time taken for ____
a) 50% conversion
b) 75% conversion
c) 20% conversion
d) 30% conversion
View Answer
Explanation: Half Life is the time to reduce the reactant concentration to half of initial value. Hence, 50% of the reactant is converted to product.
3. For all orders of reaction except the first order, half life is related to initial concentration as ____
a) t0.5 α CAon
b) t0.5 α CAo1-n
c) t0.5 α CAo2n
d) t0.5 α CAo
View Answer
Explanation: The generalised equation is t0.5 = \(\frac{C_{A0}^{1-n}(2^{n-1}- 1)}{(n-1)k}.\) At half life time, for a reaction of order n, CA = 0.5CAo.
4. The plot representing the relationship between ln(t0.5) and ln(CAo) for second order reaction is ___
a) 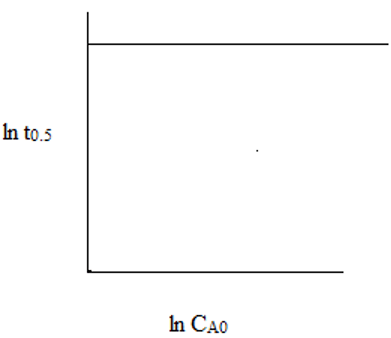
b) 
c) 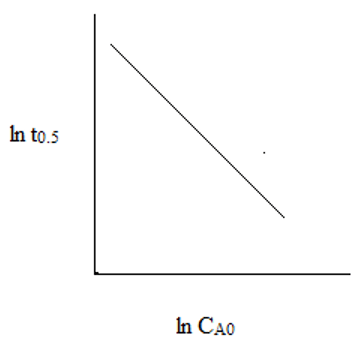
d) 
View Answer
Explanation: The slope of the line is (1 – 2) = -1. Hence, the straight line is linearly decrementing.
5. The relationship between t.0.5 and CAo for a zero order reaction is ____
a) t0.5 = \(\frac{1}{kC_{A0}} \)
b) t0.5 = \(\frac{1}{C_{A0}} \)
c) t0.5 = \(\frac{C_{A0}}{k}\)
d) t0.5 = \(\frac{C_{A0}}{2k}\)
View Answer
Explanation: For zero order reaction, \(\frac{-dC_A}{dt}\) = k. t0.5 = \(\frac{C_{A0}- \frac{C_{A0}}{2}}{k}.\)
Hence, t0.5 = \(\frac{C_{A0}}{2k}.\)
6. For a zero order reaction, the slope of t0.5 and CAo is ____
a) 2
b) 3
c) 1
d) 0
View Answer
Explanation: Slope is (1-n). At n=0, slope = 1.
7. What is the slope of the plot of ln (t0.5) and ln (CAo)? (Where n is the reaction order)
a) 1-n
b) 2-n
c) n
d) \(\frac{n}{2} \)
View Answer
Explanation: The plot is a straight line of slope (1-n). The equation representing the relationship is ln (t0.5) = ln\((\frac{(2^{n-1}-1)}{(n-1)k})\) + (1 – n) ln (CAo).
8. If t0.5 = 100 minutes and initial concentration is 10, then the order of the reaction is ____
a) 4
b) -1
c) -2
d) 1
View Answer
Explanation: t0.5 = \(C_{A0}^{1-n}.\)100 = 10(1 – n). Hence, n = -1.
9. The fractional conversion is expressed as____
a) \(\frac{C_A}{C_{A0}} \)
b) \(\frac{C_{A0}}{C_A} \)
c) \(\frac{1}{C_{A0}} \)
d) \(\frac{C_A}{kC_{A0}} \)
View Answer
Explanation: Fractional conversion is the time required to reduce the concentration to any fraction. It is the ratio of final to initial concentration.
10. The time required to convert to a fraction of 0.7 for a first order reaction is ____
a) t0.7 = \(\frac{(0.7)}{C_{A0} k}\)
b) t0.7 = \(\frac{(-0.7)}{C_{A0} k}\)
c) t0.7 = \(\frac{(0.3)}{C_{A0} k}\)
d) t0.7 = \(\frac{(-0.3)}{C_{A0} k}\)
View Answer
Explanation: The time for converting to any fraction, F is, tF = \(\frac{C_{A0}^{1-n}(F^{n-1}-1)}{(n-1)k}.\) At F = 0.7, t0.7 = \(\frac{C_{A0}^{1-2}(0.7^1- 1)}{k}.\)
Sanfoundry Global Education & Learning Series – Chemical Reaction Engineering.
To practice all areas of Chemical Reaction Engineering for Aptitude test, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Apply for Chemical Engineering Internship
- Practice Chemical Engineering MCQs
- Check Chemical Reaction Engineering Books
- Apply for Biotechnology Internship
- Check Chemical Engineering Books
