Merge Sort Program in C with Example

Problem Description

Write a C program to perform a merge sort using recursion and function.

What is Merge Sort?

Merge Sort is a divide and conquer-based sorting algorithm. In this sorting algorithm the unsorted array keeps on dividing into two halves until the array is either empty or contains only one element, which is the base case of Merge Sort, and then the halves are combined/Merged in sorted order producing a sorted array. It is one of the most popular and efficient sorting techniques.

Problem Solution

Example:

If the input array is {7, 2, 3, 10, 1, 0, 6, 9}

the expected output array will have data as {0, 1, 2, 3, 6, 7, 9, 10}

Complete Approach of Merge Sort:

Consider an unsorted array as shown in the figure.

Merge Sort Algorithm

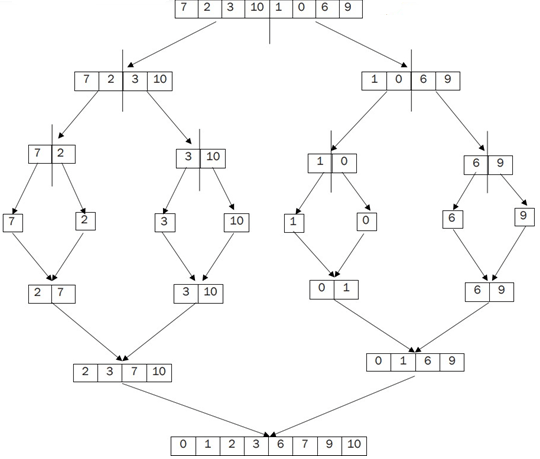
Start
1. Declare Array, left, right and mid variables
2. Find mid by formula mid = (left+right)/2
3. Call MergeSort for the left to mid
4. Call MergeSort for mid+1 to right
5. Continue step 2, 3, and 4 while the left is less than the right
6. Then Call the Merge function
End

There are several ways to write an merge sort program in C language. Let’s discuss all the ways in detail.

Merge Sort Program in C using Recursion and Function
Merge Sort Program in C using Linked List

Subscribe Now: C Algorithms Newsletter | Important Subjects Newsletters

Method 1: (Using Recursion and Function)

In this method, we use recursion and function to sort an array of numbers using the merge sort algorithm.

Program/Source Code

Here is the source code of the C program to sort an array of integers using Merge Sort Algorithm. The C program is successfully compiled and run on a Linux system. The program output is also shown below.

```
/*
```

 * C Program to Perform Merge Sort using Recursion and Functions

```
 */
```
```
 
```
```
#include <stdio.h>
```
```
#include <stdlib.h>
```
```
 
```
```
// merge function
```

void Merge(int arr[], int left, int mid, int right)

```
{
```
```
    int i, j, k;
```
```
    int size1 = mid - left + 1;
```
```
    int size2 = right - mid;
```
```
 
```
```
    // created temporary array
```
```
    int Left[size1], Right[size2];
```
```
 
```

    // copying the data from arr to temporary array

```
    for (i = 0; i < size1; i++)
```
```
        Left[i] = arr[left + i];
```
```
 
```
```
    for (j = 0; j < size2; j++)
```
```
        Right[j] = arr[mid + 1 + j];
```
```
 
```
```
    // merging of the array
```

    i = 0;	// intital index of first subarray

    j = 0;	// inital index of second subarray

    k = left; // initial index of parent array

```
    while (i < size1 && j < size2)
```
```
    {
```
```
        if (Left[i] <= Right[j])
```
```
        {
```
```
            arr[k] = Left[i];
```
```
            i++;
```
```
        }
```
```
        else
```
```
        {
```
```
            arr[k] = Right[j];
```
```
            j++;
```
```
        }
```
```
        k++;
```
```
    }
```
```
 
```

    // copying the elements from Left[], if any

```
    while (i < size1)
```
```
    {
```
```
        arr[k] = Left[i];
```
```
        i++;
```
```
        k++;
```
```
    }
```
```
 
```

    // copying the elements from Right[], if any

```
    while (j < size2)
```
```
    {
```
```
        arr[k] = Right[j];
```
```
        j++;
```
```
        k++;
```
```
    }
```
```
}
```
```
 
```
```
//merge sort function
```

void Merge_Sort(int arr[], int left, int right)

```
{
```
```
    if (left < right)
```
```
    {
```
```
 
```

        int mid = left + (right - left) / 2;

```
 
```

        // recursive calling of merge_sort

```
        Merge_Sort(arr, left, mid);
```

        Merge_Sort(arr, mid + 1, right);

```
 
```
```
        Merge(arr, left, mid, right);
```
```
    }
```
```
}
```
```
 
```
```
// driver code
```
```
int main()
```
```
{
```
```
    int size;
```
```
    printf("Enter the size: ");
```
```
    scanf("%d", &size);
```
```
 
```
```
    int arr[size];
```

    printf("Enter the elements of array: ");

```
    for (int i = 0; i < size; i++)
```
```
    {
```
```
        scanf("%d", &arr[i]);
```
```
    }
```
```
 
```
```
    Merge_Sort(arr, 0, size - 1);
```
```
 
```
```
    printf("The sorted array is: ");
```
```
    for (int i = 0; i < size; i++)
```
```
    {
```
```
        printf("%d ", arr[i]);
```
```
    }
```
```
    printf("\n");
```
```
    return 0;
```
```
}
```

Program Explanation

1. The MergeSort function takes the value of the minimum and maximum index of the array
2. It calculates the mid by the formula (low+high)/2 and recursively calls itself for low to mid and mid+1 to high and then calls the merge function to merge the sorted array.
3. The Merge function merges the two arrays by comparing the value in each and taking the minimum value in the newly created auxiliary array.
4. At last, whichever array is non-empty its value is just copied in the auxiliary array.
5. In the Driver Program user just declare the array and takes the input and calls the Merge Sort and merge function as shown in the code and prints the sorted result using for loop.

Time Complexity: O(nlogn)
Time Complexity of Merge Sort is O(nlogn) for best, average, and worst case.

Space Complexity: O(n)
Space Complexity of Merge Sort using an array is O(n), because Merge Sort requires an Auxiliary/temporary array for copying the elements.

Runtime Test Cases

Here’s the run time test cases for Merge sort algorithm for 3 different input cases.

Test Case 1 – Average Case: Here, the elements are entered in random order.

/* Average case */
Enter the size: 8
Enter the elements of array: 7 2 3 10 1 0 6 9
The sorted array is: 0 1 2 3 6 7 9 10

Test Case 2 – Best Case: Here, the elements are already sorted.

/* Best case */
 
Enter the size: 5
Enter the elements of array: -7 -3 8 9 12
The sorted array is: -7 -3 8 9 12

Test Case 3 – Worst Case: Here, the elements are reverse sorted.

/* Worst case */
 
Enter the size: 4
Enter the elements of array: 84 32 3 -9
The sorted array is: -9 3 32 84

Method 2: (Using Linked List)

In this method, an integer linked list is sorted using the merge sort technique.

A linked list cannot be accessed randomly and because of this slow access time, sorting algorithms like quick sort cannot be applied to it. So we use merge sort for this purpose. It works on divide and conquer technique.

Program/Source Code

Here is the source code of the C program to sort integers using Merge Sort on linked list technique. The C program is successfully compiled and run on a Linux system. The program output is also shown below.

```
#include<stdio.h>
```
```
#include<stdlib.h>
```
```
 
```
```
struct node
```
```
{
```
```
    int data;
```
```
    struct node* next;
```
```
};
```
```
 
```

struct node* sortedmerge(struct node* a, struct node* b);

void frontbacksplit(struct node* source, struct node** frontRef, struct node** backRef);

```
 
```
```
 
```
```
void mergesort(struct node** headRef)
```
```
{
```
```
    struct node* head = *headRef;
```
```
    struct node* a;
```
```
    struct node* b;
```

    if ((head == NULL) || (head -> next == NULL))

```
    {
```
```
        return;
```
```
    }
```
```
    frontbacksplit(head, &a, &b);
```
```
    mergesort(&a);
```
```
    mergesort(&b);
```
```
    *headRef = sortedmerge(a, b);
```
```
}
```
```
 
```

struct node* sortedmerge(struct node* a, struct node* b)

```
{
```
```
    struct node* result = NULL;
```
```
 
```
```
    if (a == NULL)
```
```
        return(b);
```
```
    else if (b == NULL)
```
```
        return(a);
```
```
 
```
```
    if ( a-> data <= b -> data)
```
```
    {
```
```
        result = a;
```

        result -> next = sortedmerge(a -> next, b);

```
    }
```
```
    else
```
```
    {
```
```
        result = b;
```

        result -> next = sortedmerge(a, b -> next);

```
    }
```
```
    return(result);
```
```
}
```
```
 
```

void frontbacksplit(struct node* source, struct node** frontRef, struct node** backRef)

```
{
```
```
    struct node* fast;
```
```
    struct node* slow;
```

    if (source==NULL || source->next==NULL)

```
    {
```
```
        *frontRef = source;
```
```
        *backRef = NULL;
```
```
    }
```
```
    else
```
```
    {
```
```
        slow = source;
```
```
        fast = source -> next;
```
```
        while (fast != NULL)
```
```
        {
```
```
            fast = fast -> next;
```
```
            if (fast != NULL)
```
```
            {
```
```
                slow = slow -> next;
```
```
                fast = fast -> next;
```
```
            }
```
```
    }
```
```
 
```
```
    *frontRef = source;
```
```
    *backRef = slow -> next;
```
```
    slow -> next = NULL;
```
```
    }
```
```
}
```
```
 
```
```
void printlist(struct node *node)
```
```
{
```
```
    while(node != NULL)
```
```
    {
```
```
        printf("%d ", node -> data);
```
```
        node = node -> next;
```
```
    }
```
```
}
```
```
 
```

void push(struct node** head_ref, int new_data)

```
{
```

    struct node* new_node = (struct node*) malloc(sizeof(struct node));

```
    new_node -> data  = new_data;
```
```
    new_node->next = (*head_ref);
```
```
    (*head_ref) = new_node;
```
```
}
```
```
int main()
```
```
{
```
```
    struct node* a = NULL;
```
```
    push(&a, 15);
```
```
    push(&a, 10);
```
```
    push(&a, 5);
```
```
    push(&a, 20);
```
```
    push(&a, 3);
```
```
    push(&a, 26775);
```
```
    mergesort(&a);
```

    printf("\n Sorted Linked List is: \n");

```
    printlist(a);
```
```
    return 0;
```
```
}
```

Program Explanation

1. Return if head is NULL or the Linked List has only one element in the list
2. Divide the linked list into two halves.
frontbacksplit(head, &a, &b); (a and b are two halves)
3. Sort the two halves using mergesort(&a); and mergesort(&b);
4. SortedMerge() should be used to combine the sorted a and b, and headRef should be used to update the head reference. i.e. *headRef = sortedmerge(a, b);
5. Functions are used to print and insert the nodes in the linked list.

Time Complexity: O(nlogn)
Time Complexity of Merge Sort is O(nlogn) for best, average, and worst case.

Space Complexity: O(1)
Space Complexity of Merge Sort using Linked List is O(1), as it does not uses any auxiliary space with Linked List.

Runtime Test Cases

Sorted Linked List is:
3 5 10 15 20 26775

Conclusion:

Merge Sort is a Stable Sorting Algorithm, that is it maintains the relative order for equal values/elements.
Typically Merge Sort is not considered an in-place sorting algorithm.
Merge Sort is used in External Sorting.
External Sorting is the class of sorting algorithms that can handle a massive amount of data. It is required when data does not fit in the main memory and need to be stored in secondary memory.

Drawbacks:

For Small datasets merge sort is slower than other algorithms such as selection or insertion sort.
It requires additional space of O(n).
Even if the array is sorted Merge Sort will run completely.

To practice programs on every topic in C, please visit “Programming Examples in C”, “Data Structures in C” and “Algorithms in C”.

If you find any mistake above, kindly email to [email protected]

« Prev - Quick Sort Program in C

» Next - C Program to Merge Two Sorted Array Elements

Related Posts:

Recommended Articles: