Heap Sort in C is a comparison-based efficient sorting algorithm. It is based on a Binary Heap data structure. To understand the heap sort, we first need to know some basic terminologies related to the heap sort.
Binary Tree
In a Binary tree data structure, every element contains at most two children. Given diagram shows the binary tree.
Complete Binary Tree
It is a type of binary tree in which all the levels are completely filled except the last level i.e. leaf node. The complete binary tree is filled from the left to right. Following is an example of the complete binary tree.
Binary Heap
A binary heap is a complete binary tree in which the elements are stored in such a way that the parent node is greater or smaller than its children nodes. It is classified into two types: max-heap and min-heap.
Max Heap
In the max-heap, the parent node has a greater value than the children nodes.
Min Heap
In the min heap, the parent node contains a smaller value than its children nodes.
What is Heapify?
Heapify is the process to make the heap data structure using the binary tree. It is also used when the root node is deleted from the heap. It again rebuilds the tree which follows the condition of the heap.
Write a C program to sort the array using the heap sort and display the sorted array.
There are some operations that are needed to implement the heap sort. Here we have an array of integers that is needed to sort. We will use an array-based representation of the binary heap. In this representation, if the parent node is stored at the index i then its left child will be at 2*i + 1 and right child at 2*i + 2.
Following are the steps that should follow to implement the heap sort.
- Build a binary heap.
- Start iterating from mid to the start of the binary heap array.
- On every iteration, swap the root node with the last leaf node.
- Remove the leaf node by putting it back at the end of the new sorted array.
- Again do the heapify operation and repeat the iteration from step 2.
- Exit
Here is the source code to implement heap sort in C. Heap is built using array representation. The C program is successfully compiled and run on a Linux system. The program output is also shown below.
/** Heap Sort Program in C*/#include<stdio.h>// function prototypingvoid heapify(int*,int, int);
void heapsort(int*, int);
void print_array(int*, int);
int main()
{int arr[] = { 10, 30, 5, 63, 22, 12, 56, 33 };
int n = sizeof(arr) / sizeof(arr[0]);
printf("\nArray before sorting:\n");
print_array(arr, n);
heapsort(arr, n);
printf("\n\nArray after sorting:\n");
print_array(arr, n);
return 0;
}/* sorts the given array of n size */void heapsort(int* arr, int n)
{// build the binary max heapfor (int i = n / 2 - 1; i >= 0; i--)
{heapify(arr, n, i);
}// sort the max heapfor (int i = n - 1; i >= 0; i--)
{// swap the root node and the last leaf nodeint temp = arr[i];
arr[i] = arr[0];
arr[0] = temp;
// again heapify the max heap from the rootheapify(arr, i, 0);
}}/* heapify the subtree with root i */void heapify(int* arr, int n, int i)
{// store largest as the root elementint largest = i;
int left = 2 * i + 1;
int right = 2 * i + 2;
// now check whether the right and left right is larger than the root or notif (left < n && arr[left] > arr[largest])
{largest = left;
}if (right < n && arr[right] > arr[largest])
{largest = right;
}// if the root is smaller than the children then swap it with the largest children's valueif (largest != i)
{int temp = arr[i];
arr[i] = arr[largest];
arr[largest] = temp;
// again heapify that side of the heap where the root has goneheapify(arr, n, largest);
}}/* printf the array */void print_array(int* arr, int n)
{for (int i = 0; i < n; i++)
{printf("%d ", arr[i]);
}}
Let’s understand the Heap Sort Program in C by the given steps:
1. Print the unsorted array.
2. Creating the binary heap of the array.
3. Start iteration from the last leaf node of the heap to the root node.
4. Each iteration swaps the root node with the last leaf node and then calls the heapify operation to rearrange the heap.
5. On heapify operation, swap the larger children element with the root node if the root is smaller than the child.
6. Print the sorted array.
Now, let’s understand the working of the heap sort algorithm with the diagram.
Here we are performing basically two types of operations:
- Building the array-based max heap.
- Heapify the heap on every root and leaf node swapping.
Let’s take an example of an unsorted array that has 8 elements.
| 10 | 30 | 5 | 63 | 22 | 12 | 56 | 33 |
Step 1: Construct Max Heap from Given Array i.e. {10, 30, 5, 63, 22, 12, 56, 33}
Initially, we must construct the max heap from the given array of elements.
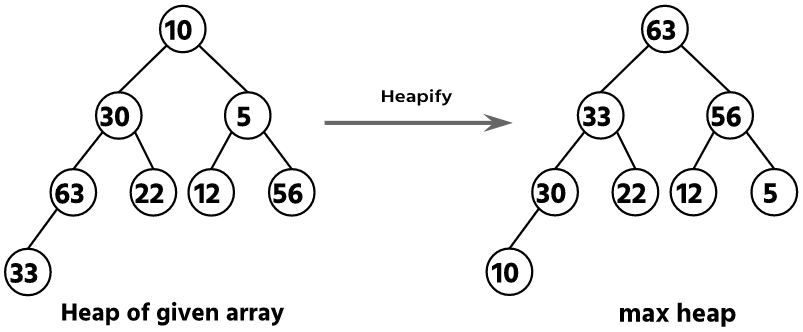
Now the given array will be changed and it is max-heap. Now the array looks like this:
| 63 | 56 | 33 | 12 | 30 | 22 | 10 | 5 |
Step 2: Delete the root node (63) & perform heapify operation.
The task is to delete the root node which is 63. To delete this node, we have to swap this node with leaf node 10 and remove the leaf node. After swapping we have to perform a heapify operation again.
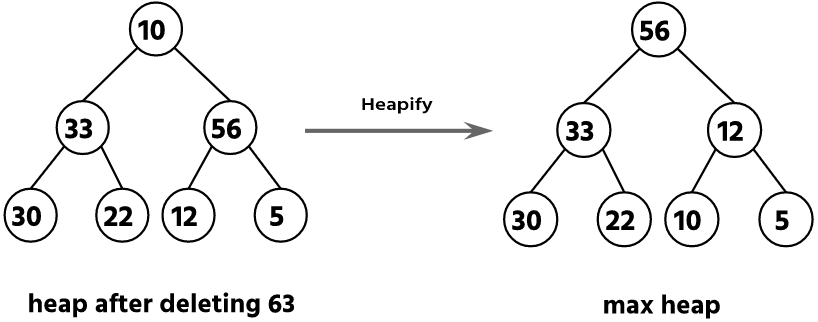
Now the array is changed, and 63 is stored at the end of the list.
| 56 | 33 | 12 | 30 | 22 | 10 | 5 | 63 |
Step 3: Delete the root node (56) & perform heapify operation.
Again, we have to delete the root element 56. To delete the root element, we have to swap the root with the leaf node having data 5. After deletion, we have to perform the heapify operation.
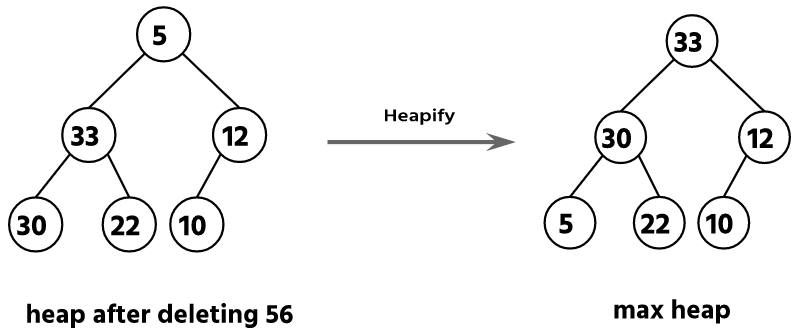
After swapping the root node and leaf node, the array of elements is changed:
| 33 | 30 | 12 | 5 | 22 | 10 | 56 | 63 |
Step 4: Delete the root node (33) & perform heapify operation.
Now, we have to delete the root node 33. To delete the root node, we have to perform a swapping operation between the root node and the leaf node 10.
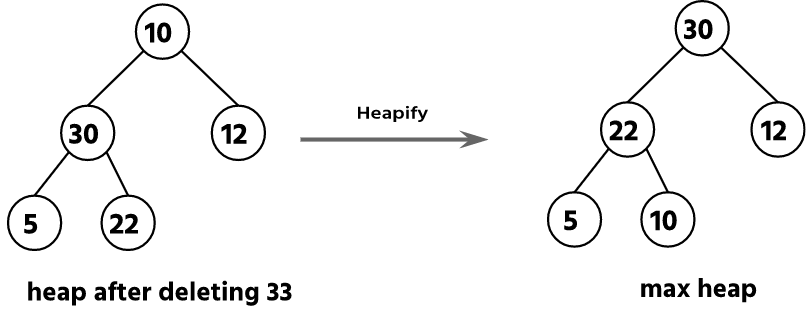
Now the array with be changed after the deletion process:
| 30 | 22 | 12 | 5 | 10 | 33 | 56 | 63 |
Step 5: Delete the root node (30) & perform heapify operation.
In this step, we have to delete the root node with data 30. To delete the root node, we have to perform the swapping operation between the root node and leaf node having data 10.
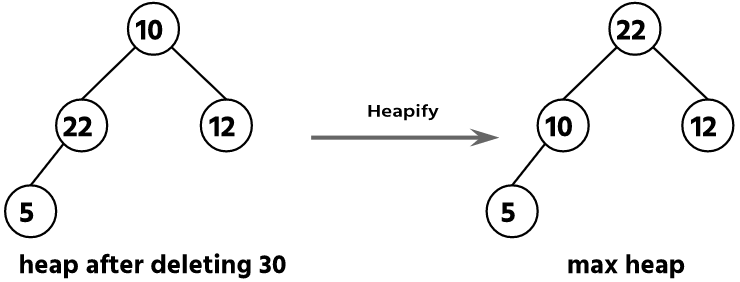
After deletion of the root node and swapping, the array is changed:
| 22 | 10 | 12 | 5 | 30 | 33 | 56 | 63 |
Step 6: Delete the root node (22) and leaf node & perform swapping operation.
In this step, delete the root node. To delete the root node, we have to swap the root node with the last leaf node 5. After swapping the leaf node, we have to heapify the heap.
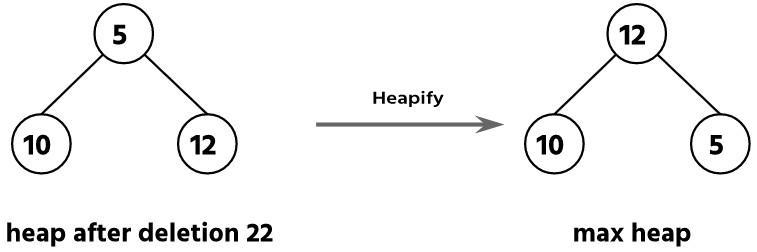
Now the array is changed after the deletion of the root and leaf node.
| 12 | 10 | 5 | 22 | 30 | 33 | 56 | 63 |
Step 7: Delete the root node (12) & perform swapping operation.
Now in this step, we have to delete the root node 12. To delete the root node, we have to swap it with leaf node 5. After swapping operations, we need to heapify the max heap.
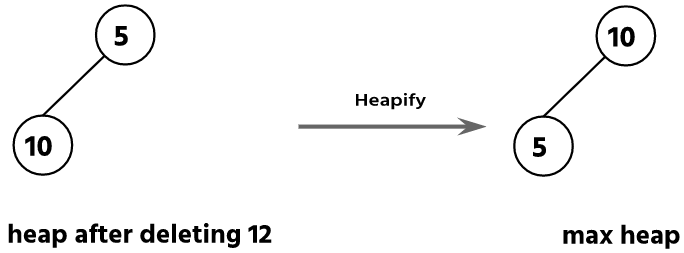
Now the array is changed after the swapping operation:
| 10 | 5 | 12 | 22 | 30 | 33 | 56 | 63 |
Step 8: Delete the root node (10) & perform heapify.
In this step, we need to delete the root node 10. To delete the root node, we have to perform the swapping operation between the two root nodes and the leaf node 5. After swapping, we do heapify.
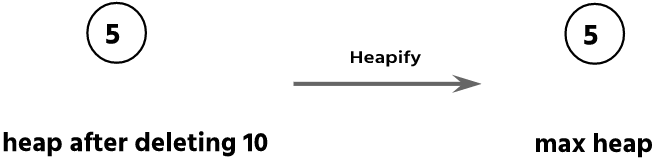
After removing the root node, the array is changed:
| 5 | 10 | 12 | 22 | 30 | 33 | 56 | 63 |
Step 9: Delete the root node.
In this step, we have to delete the root node. Since there is only one node that remains, after deleting it, the heap will be empty.
Null heap after deleting 5
Now the final sorted array is given below.
| 5 | 10 | 12 | 22 | 30 | 33 | 56 | 63 |
Time Complexity: O(n logn)
Here the traversal occurs n time, where n is the size of the array. To sort each element we need to perform a heapify operation which takes log n time.
Best case = Avg case = Worst case = O(n logn)
Space Complexity: O(1)
Since we are not using extra space to sort the list using heap sort. So space is constant.
In this case, we are performing heap sort operation. The given array has the values 10, 30, 5, 63, 22, 12, 56, and 33.
Array before sorting: 10 30 5 63 22 12 56 33 Array after sorting: 5 10 12 22 30 33 56 63
To practice programs on every topic in C, please visit “Programming Examples in C”, “Data Structures in C” and “Algorithms in C”.
If you find any mistake above, kindly email to [email protected]- Practice BCA MCQs
- Apply for C Internship
- Check C Books
- Apply for Computer Science Internship
- Check Computer Science Books
