This set of Antennas Multiple Choice Questions & Answers (MCQs) focuses on “Factors”.
1. The normalized array factor of a two element array antenna is given by ___________
a) \(AF_n=cos(\frac{kdcosθ+β}{2})\)
b) \(AF_n=2cos(\frac{kdcosθ+β}{2})\)
c) \(AF_n=cos(\frac{kdcosθ}{2}+β)\)
d) \(AF_n=cos(\frac{kdsinθ+β}{2})\)
View Answer
Explanation: Array factor is the function of antenna positions in the array and its weights. The array factor for a two element array antenna is given by \(AF=2cos(\frac{kdcosθ+β}{2})\)
The normalized array factor is given by \(AF_n=\frac{AF}{2}=cos(\frac{kdcosθ+β}{2}).\)
2. Which of the following is a function of position of antennas in array and the weights?
a) Array Factor
b) Field pattern
c) Total array field
d) Beamwidth
View Answer
Explanation: Array factor is the function of antenna positions in the array and its weights. The normalized array factor is given by \(AF_n=\frac{AF}{2}=cos(\frac{kdcosθ+β}{2})\). Field pattern is multiplication of single element with the array factor. Total array field is the field generated by the sum of the individual elements in array.
3. Find the normalized Array factor when two antenna elements are separated by a distance of λ/4 and phase difference is 0 and θ=0?
a) \(cos(\frac{π}{4})\)
b) \(cos(\frac{π}{2})\)
c) \(cos(\frac{3π}{4})\)
d) \(cos(\frac{3π}{2})\)
View Answer
Explanation: The normalized array factor is given by \(AF_n=\frac{AF}{2}=cos(\frac{kdcosθ+β}{2})\)
⇨ \(AF_n=cos(\frac{kdcosθ+β}{2})=cos(\frac{(\frac{2π}{λ})(λ/4)cosθ+0}{2})=cos(\frac{π}{4})\)
4. Which of the following pattern represents the array factor of a two element array separated by a distance of λ/4 and phase difference is 0?
a) 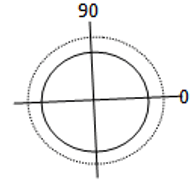
b) 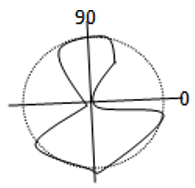
c) 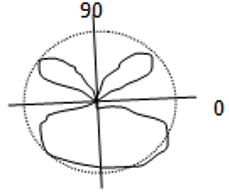
d) 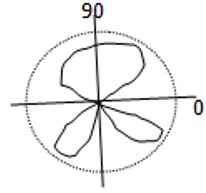
View Answer
Explanation: The normalized array factor is given by \(AF_n=\frac{AF}{2}=cos(\frac{kdcosθ+β}{2})\)
⇨ AFn=0
⇨ \(cos(\frac{kdcosθ+β}{2})=0\)
⇨ \(\frac{(\frac{2π}{λ})(λ/4)cosθ+0}{2})=\frac{π}{2}\)
⇨ cosθ=2
No Nulls will occur for the given pattern. So the pattern is represented as

5. Which of the following is true for uniform linear array elements, to obtain the total field?
a) The single element field is multiplied by the array factor
b) The single element field is multiplied by the normalized array factor
c) The single element field is multiplied by the beamwidth
d) The single element field is multiplied by the directivity
View Answer
Explanation: Total array field is the field generated by the sum of the individual elements in array and is given simple by multiplying the field due to single element by the array factor. Array factor is the function of antenna positions in the array and its weights. Multiplying the normalized field with the normalized array factor gives the pattern multiplication.
6. Multiplying the normalized field with the normalized array factor gives ___________
a) pattern multiplication
b) array factor
c) beamwidth
d) null
View Answer
Explanation: The radiation pattern of the single array antenna is multiplied by the antenna factor then it is called pattern multiplication. So multiplying the normalized field with the normalized array factor gives the pattern multiplication. Array factor is the function of antenna positions in the array and its weights. Nulls are known by equating array factor to zero.
7. Find the angle at which nulls occur for the two element array antenna with separation λ/4 and phase difference is π/2?
a) 0
b) π/2
c) π/4
d) π
View Answer
Explanation: The normalized array factor is given by \(AF_n=\frac{AF}{2}=cos(\frac{kdcosθ+β}{2})\)
⇨ AFn=0
⇨ \(cos(\frac{kdcosθ+β}{2})=0\)
⇨ \(\frac{(\frac{2π}{λ})(λ/4)cosθ+\frac{π}{2}}{2}=\frac{π}{2}\)
⇨ Cosθ=1
⇨ θ=0
So Nulls occur at 0°.
8. Find the angle at which nulls occur for the two element array antenna with separation λ/4 and phase difference is -π/2?
a) 0
b) π/2
c) π/4
d) π
View Answer
Explanation: The normalized array factor is given by \(AF_n=\frac{AF}{2}=cos(\frac{kdcosθ+β}{2})\)
⇨ AFn=0
⇨ \(cos(\frac{kdcosθ+β}{2})=0\)
⇨ \(\frac{(\frac{2π}{λ})(\frac{λ}{4})cosθ-\frac{π}{2}}{2}=±\frac{π}{2}\)
⇨ Cosθ=-1
⇨ θ=180 or π
So Nulls occur at 180°.
9. Find the angle at which nulls occur for the two element array antenna with separation λ/4 and phase difference is 0?
a) Doesn’t exist
b) 0
c) π/2
d) π/4
View Answer
Explanation: The normalized array factor is given by \(AF_n=\frac{AF}{2}=cos(\frac{kdcosθ+β}{2})\)
⇨ AFn=0
⇨ \(cos(\frac{kdcosθ+β}{2})=0\)
⇨ \(\frac{(\frac{2π}{λ})(λ/4)cosθ+0}{2}=\frac{π}{2}\)
⇨ cosθ=2
No Nulls will occur for the given pattern.
10. For N- element linear uniform array, the normalized array factor is represented as ______________
a) \(\frac{sin(Nᴪ/2)}{Nᴪ/2}\)
b) \(\frac{cos(Nᴪ/2)}{Nᴪ/2}\)
c) \(N\frac{sin(ᴪ/2)}{ᴪ/2}\)
d) \(N\frac{cos(Nᴪ/2)}{Nᴪ/2}\)
View Answer
Explanation: The N-element linear uniform array, having a constant phase difference will have the array factor AF = \(∑_{n=1}^Ne^{j(n-1)ᴪ}\)
Normalized array factor is given by \(\frac{sin(Nᴪ/2)}{Nᴪ/2}\)
Sanfoundry Global Education & Learning Series – Antennas.
To practice all areas of Antennas, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Electrical Engineering Books
- Apply for Electronics & Communication Engineering Internship
- Practice Electronics & Communication Engineering MCQs
- Practice Electrical Engineering MCQs
- Apply for Electrical Engineering Internship
