This set of Analog Circuits Multiple Choice Questions & Answers (MCQs) focuses on “Low Frequency Response and Miller Effect Capacitance”.
1. In Miller’s theorem, what is the constant K?
a) Total voltage gain
b) Internal voltage gain
c) Internal current gain
d) Internal power gain
View Answer
Explanation: The constant K=V2/V1, which is the internal voltage gain of the network.
Thus resistance RM=R/1-K
RN=R/1-K-1.
2. When applying miller’s theorem to resistors, resistance R1 is for node 1 and R2 for node 2. If R1>R2, then for same circuit, then for capacitance for which the theorem is applied, which will be larger, C1 or C2?
a) C1
b) C2
c) Both are equal
d) Insufficient data
View Answer
Explanation: Given R1>R2
R/1-K > R/1-K-1, and so 1-K-1>1-K
Thus K2>1, K>1, K<-1 (correct)
Thus, C1=C(1-K) and C2=C(1-K-1)
Hence C1>C2.
3. Find net voltage gain, given hfe = 50 and hie = 1kΩ.

a) 27.68
b) -22
c) 30.55
d) -27.68
View Answer
Explanation: Apply millers theorem to resistance between input and output.
At input, RM=100k/1-K = RI
Output, RN=100k/1-K-1 ≈ 100k
Internal voltage gain , K = -hfeRL’/hie
K = – 50xRc||100k/1k = – 50x4x100/104 = – 192
RI = 100k/1+192 = 0.51kΩ
RI’ = RI||hie = 0.51k||1k = 0.51×1/1.51 = 0.337kΩ
Net voltage gain = K.RI’/RS+RI’ = – 192 x 0.337/2k + 0.337k = -27.68.
4. Given that capacitance w.r.t the input node is 2pF and output node is 4pF, find capacitance between input and output node.
a) 0.67 pF
b) 1.34pF
c) 0.44pF
d) 2.2pF
View Answer
Explanation: C1=C(1-K), C2=C(1-K-1)
C1=2pF
C2=4pF
C1/C2=1/2=1-K/1-K-1
K = -2
C1 = C(1+2) = 3C
C = C1/3 = 2/3pF = 0.67 pF.
5. Consider an RC coupled amplifier at low frequency. Internal voltage gain is -120. Find the voltage gain magnitude, when given that collector resistance = 1kΩ, load = 9kΩ, collector capacitance is 0. is 0.1μF, and input frequency is 20Hz.
a) 120
b) 12
c) 15
d) -12
View Answer
Explanation: AV = -120
fL = 1/2πCC(RC+RL) = 1/2π*0.001 = 1000/2π = 159.15Hz
AV’ = \(\frac{|AV|}{\sqrt{1}} + (\frac{f_L}{f})^2\)
AV’ = 120/8.02 ≈ 15.
6. Find the 3-dB frequency given that the gain of RC coupled amplifier is 150, the low frequency voltage gain is 100 and the input frequency is 50Hz.
a) 50.8 Hz
b) 55.9 Hz
c) 60Hz
d) 100Hz
View Answer
Explanation: AVM = 150
AVL = 100
f = 50Hz
100 = \(\frac{150}{\sqrt{1}}+(\frac{f_L}{50})^2\)
1+f2/2500 = 1.52
f2 = 2500*1.25 = 3125
f = 55.90 Hz.
7. Given collector resistance = 2kΩ, load resistance = 5kΩ, collector capacitance = 1μF, emitter capacitance = 20μF, collector current = 2mA, source resistance = 2kΩ. If the effect of blocking capacitor is ignored, find the applicable cut-off frequency.
a) 22.73 Hz
b) 612 Hz
c) 673Hz
d) 317 Hz
View Answer
Explanation: RC = 2kΩ, RL = 5kΩ, CC = 1μF, CB = 10μF, CE = 20μF, RS = 2 kΩ
hie = 1kΩ, IC = 2mA
fL1 = 1/2πCC(RC+RL) = 22.73 Hz
fL2 = gm/2πCE = IC/2πCEVT = 612 Hz
Since fL2 > 4fL1, hence fL2 is the correct answer.
8. Consider the circuit shown.
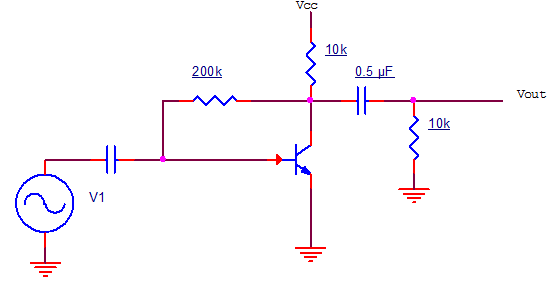
hfe = 50, hie = 1000Ω. Find magnitude of voltage gain at input frequency 10Hz.
a) 100
b) 133
c) 166
d) 220
View Answer
Explanation: Net load = 10k||10k = 5kΩ = RL’
AVM = -hfeRL’/hie = -50×5/1 = -250
fL = 1/2πCC(RC+RL) = 15.9 Hz
AVL = \(\frac{AVM}{\sqrt{1}} + (\frac{fL}{f})^2\) = 133.
9. What is the phase shift in RC coupled CE amplifier at lower 3dB frequency?
a) 180°
b) 225°
c) 270°
d) 100°
View Answer
Explanation: Total phase shift = 180°+ tan-1(fL/f)
At 3dB frequency fL/f = 1
Total phase shift = 180° + 45° = 225°.
10. Consider that the phase shift of an RC coupled CE amplifier is 260°. Find the low frequency gain when the voltage gain of the transistor is -150.
a) 100
b) 26
c) 40
d) 55
View Answer
Explanation: 180° + tan-1(fL/f) = 260°
fL/f = tan(80) = 5.67
A = \(\frac{150}{\sqrt{1}}\) + 5.672 = 26.05.
Sanfoundry Global Education & Learning Series – Analog Circuits.
To practice all areas of Analog Circuits, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
