This set of Advanced Surveying Questions and Answers focuses on “Triangulation – Satellite Station: Reduction to Centre “.
1. Which of the following can describe the main purpose of the satellite station?
a) Act as false station
b) Act as true station
c) Measuring length
d) Measuring diameter
View Answer
Explanation: The main purpose of the satellite station is to act as an eccentric station or a false station. For securing well conditioned triangle some of the objects like flag poles, towers, were chosen as satellite station.
2. The recordings taken from eccentric station are more precise.
a) False
b) True
View Answer
Explanation: Satellite station involves in adopting the place where instrument can’t be placed. So, this might have an opportunity to create error in the recordings taken which can be further removed by applying corrections. The recordings taken are near to precise value.
3. Which of the following indicates the formula of phase correction?
a) β = 206265 + d * sin (γ) / a
b) β = 206265 * d – sin (γ) / a
c) β = 20265 * d * sin (γ) / a
d) β = 206265 * d * sin (γ) / a
View Answer
Explanation: The phase correction is actually used for determining the eccentricity of the signal. The observations of this signal can be made by placing the station out of the center, which is essential to correct the angles, which is similar to the corrections of satellite station.
4. Which of the following method can be adopted if there is any object in the point of instrument station?
a) Centric station
b) True station
c) Satellite station
d) Controlled station
View Answer
Explanation: The main objective of using satellite station is to place the instrument in the surrounding places of the point where object has been pre constructed. This involves in enhancing technical knowledge and also in improving false stations.
5. Find the true angle from the given figure.
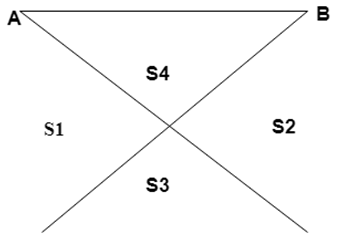
a) α = θ + β1 – β2
b) α = θ + β1 + β2
c) α = θ – β1 – β2
d) α = θ * β1 – β2
View Answer
Explanation: The true angle can be calculated by determining the positions of the station points and the remaining points. From the figure, at position S1, the true angle is given as
α = θ + β1 – β2.
6. Determine the true angle, if the station is placed at the second point having angles θ, α and β as 20˚45ꞌ, 2˚31ꞌ and 7˚12ꞌ.
a) 52˚26ꞌ
b) 25˚62ꞌ
c) 25˚26ꞌ
d) 26˚25ꞌ
View Answer
Explanation: The value of the true angle at the second station point can be determined by
Angle = θ – α + β. On substitution, we get
Angle = 20˚45ꞌ – 2˚31ꞌ + 7˚12ꞌ
True angle = 25˚26ꞌ.
7. Determine the eccentric station point if the station is 1.65m to the west and the distance between remaining two station points is given as 300m, with an angle of 10˚12ꞌ.
a) 200˚35ꞌ
b) 2˚53ꞌ
c) 202˚53ꞌ
d) 200˚53ꞌ
View Answer
Explanation: The value of eccentric station can be found out by using,
β = 206265*d*sin (γ) / a. On substitution, we get
β = 206265*1.65*sin (10˚12ꞌ) / 300
β = 200˚53ꞌ.
8. Determine the corrected direction of the eccentric station if the value of D is given as 200m with a reflection of 9˚15ꞌ having a distance of 1.2m from the main station.
a) 198˚45ꞌ
b) 198˚56ꞌ
c) 189˚56ꞌ
d) 918˚56ꞌ
View Answer
Explanation: The corrected direction of the eccentric station can be determined by
β = d*sin θ*206265 / D. On substitution, we get
β = 1.2*sin 9˚15ꞌ*206265 / 200
β = 198˚56ꞌ.
9. Calculate the corrected angle if the values of θ, β1 and β2 are given as 50˚46ꞌ, 12˚24ꞌ and 13˚36ꞌ.
a) 94˚34ꞌ
b) 49˚43ꞌ
c) 4˚34ꞌ
d) 49˚34ꞌ
View Answer
Explanation: The corrected angle can be determined by using the formula,
Corrected angle = θ + β1 – β2. On substitution, we get
Corrected angle = 50˚46ꞌ + 12˚24ꞌ – 13˚36ꞌ
Corrected angle = 49˚34ꞌ.
10. Satellite station is also known as__________
a) Centric station
b) True station
c) Eccentric station
d) Instrument station
View Answer
Explanation: A satellite station can also be known as an eccentric station. It involves the following process when a structure is taken as an instrument station, it is not possible to set the instrument over that structure and a false station point is assumed that can be referred as satellite station.
Sanfoundry Global Education & Learning Series – Surveying.
To practice advanced questions and answers on all areas of Surveying, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Apply for Civil Engineering Internship
- Check Surveying Books
- Check Civil Engineering Books
- Practice Civil Engineering MCQs
