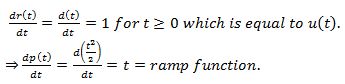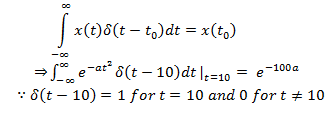This set of Signals & Systems Multiple Choice Questions & Answers (MCQs) focuses on “Useful Signals”.
1. What is the value of d[0], such that d[n] is the unit impulse function?
a) 0
b) 0.5
c) 1.5
d) 1
View Answer
Explanation: The unit impulse function has value 1 at n = 0 and zero everywhere else.
2. What is the value of u[1], where u[n] is the unit step function?
a) 1
b) 0.5
c) 0
d) -1
View Answer
Explanation: The unit step function u[n] = 1 for all n>=0, hence u[1] = 1.
3. Evaluate the following function in terms of t: {sum from -1 to infinity:d[n]}/{Integral from 0 to t: u(t)}
a) t
b) 1⁄t
c) t2
d) 1⁄t2
View Answer
Explanation: The numerator evaluates to 1, and the denominator is t, hence the answer is 1/t.
4. Evaluate the following function in terms of t: {integral from 0 to t}{Integral from -inf to inf}d(t)
a) 1⁄t
b) 1⁄t2
c) t
d) t2
View Answer
Explanation: The first integral is 1, and the overall integral evaluates to t.
5. The fundamental period of exp(jwt) is
a) pi/w
b) 2pi/w
c) 3pi/w
d) 4pi/w
View Answer
Explanation: The function assumes the same value after t+2pi/w, hence the period would be 2pi/w.
6. Find the magnitude of exp(jwt). Find the boundness of sin(t) and cos(t).
a) 1, [-1,2], [-1,2]
b) 0.5, [-1,1], [-1,1]
c) 1, [-1,1], [-1,2]
d) 1, [-1,1], [-1,1]
View Answer
Explanation: The sin(t)and cos(t) can be found using Euler’s rule.
7. Find the value of {sum from -inf to inf} exp(jwn)*d[n].
a) 0
b) 1
c) 2
d) 3
View Answer
Explanation: The sum will exist only for n = 0, for which the product will be 1.
8. Compute d[n]d[n-1] + d[n-1]d[n-2] for n = 0, 1, 2.
a) 0, 1, 2
b) 0, 0, 1
c) 1, 0, 0
d) 0, 0, 0
View Answer
Explanation: Only one of the values can be one at a time, others will be forced to zero, due to the delta function.
9. Defining u(t), r(t) and s(t) in their standard ways, are their derivatives defined at t = 0?
a) Yes, Yes, No
b) No, Yes, No
c) No, No, Yes
d) No, No, No
View Answer
Explanation: None of the derivatives are defined at t=0.
10. Which is the correct Euler expression?
a) exp(2jt) = cos(2t) + jsin(t)
b) exp(2jt) = cos(2t) + jsin(2t)
c) exp(2jt) = cos(2t) + sin(t)
d) exp(2jt) = jcos(2t) + jsin(t)
View Answer
Explanation: Euler rule: exp(jt) = cos(t) + jsin(t).
11. The range for unit step function for u(t – a), is ________
a) t < a
b) t ≤ a
c) t = a
d) t ≥ a
View Answer
Explanation: A unit step signal u(t) = 1 when t ≥ 0 and 0 when t < 0
∴ u(t – a) = 1 when t – a ≥ 0 ⇒ t ≥ a
12. Which one of the following is not a ramp function?
a) r(t) = t when t ≥ 0
b) r(t) = 0 when t < 0
c) r(t) = ∫u(t)dt when t < 0
d) r(t) = du(t)⁄dt
View Answer
Explanation: Ramp function r(t) = t when t ≥ 0 and r(t) = 0 when t < 0
Also, r(t)= ∫u(t)dt = ∫dt = t (∵u(t) = 1 for t≥0)
⇒ du(t)⁄dt = d(1)⁄dt = 0 which is not a ramp function.
13. Which one of the following is not a unit step function?
a) u(t)=1 for t ≥ 0
b) u(t)=0 for t < 0
c) u(t)=\(\frac{dr(t)}{dt}\) for t ≥ 0
d) u(t)=\(\frac{dp(t)}{dt}\) for t ≥ 0
View Answer
Explanation: Unit step function, u(t) = 1 for t ≥ 0 and u(t) = 0 for t < 0. Also,
14. Unit Impulse function is obtained by using the limiting process on which among the following functions?
a) Triangular Function
b) Rectangular Function
c) Signum Function
d) Sinc Function
View Answer
Explanation: Unit impulse function can be obtained by using a limiting process on the rectangular pulse function. Area under the rectangular pulse is equal to unity.
15. Evaluate: 
a) {2,1.5,0,6}
b) {2,1.5,6,0}
c) {2,0,1.5,6}
d) {2,1.5,0,3}
View Answer
Explanation: From the impulse function property,
16. When is a complex exponential signal pure DC?
a) σ = 0 and Ω < 0
b) σ < 0 and Ω = 0
c) σ = 0 and Ω = 0
d) σ < 0 and Ω < 0
View Answer
Explanation: A complex exponential signal is represented as x(t)= est
Where, s = σ + jΩ
⇒ x(t) = eσt [cosΩt + jsinΩt] When, σ = 0 and Ω = 0 ⇒ x(t) = e0 [cos0 + jsin0] = 1 × 1 = 1 which is pure DC.
Sanfoundry Global Education & Learning Series – Signals & Systems.
To practice all areas of Signals & Systems, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
