This set of Network Theory Multiple Choice Questions & Answers (MCQs) focuses on “The Impulse Function in Circuit Analysis”.
1. For the circuit shown below, find the voltage across the capacitor C1 at the time the switch is closed.
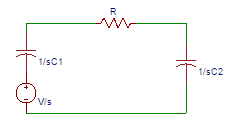
a) 0
b) V/4
c) V/2
d) V
View Answer
Explanation: We use two different cicuits to illustrate how an impulse function can be created with a switching operation. The capacitor is charged to an initial voltage of V at the time the switch is closed.
2. The charge on capacitor C2 in the circuit shown below is?

a) 0
b) 1
c) 2
d) 3
View Answer
Explanation: In the circuit, the initial charge on C2 is zero. So, charge on capacitor C2 = zero. Capacitor circuit and series inductor circuit are two different cicuits to illustrate how an impulse function can be created with a switching operation.
3. The current in the circuit shown below is?

a) (V/R)/(s+1/Ce)
b) (V/R)/(s+1/RCe)
c) (V/R)/(s-1/RCe)
d) (V/R)/(s-1/Ce)
View Answer
Explanation: The current flowing through the circuit is given by I = (V/s)/(R+1/sC1+1/sC2) = (V/R)/(s+1/RCe) where the equivalent capacitance C1C2/(C1+C2) and is replaced by Ce.
4. By taking the inverse transform of the current (V/R)/(s+1/RCe), the value of the current is?

a) V/R et/Ce
b) V/R et/RCe
c) V/R e-t/RCe
d) V/R e-t/Ce
View Answer
Explanation: By taking the inverse transform of the current, we obtain i = V/R e-t/RCe which indicates that as R decreases, the initial current increases and the time constant decreases.
5. Consider the circuit shown below. On applying the Kirchhoff’s current law, the equation will be?
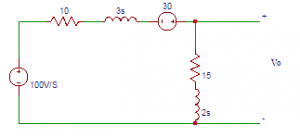
a) V/(2s-15)+(V-[(100/s)+30])/(3s+10)=0
b) V/(2s-15)+(V-[(100/s)+30])/(3s-10)=0
c) V/(2s+15)+(V-[(100/s)+30])/(3s+10)=0
d) V/(2s+15)+(V-[(100/s)+30])/(3s-10)=0
View Answer
Explanation: The current in the 3H inductor at t = 0 is 10A and the current in 2H inductor at t = 0 is zero. Applying Kirchhoff’s current law, we get V/(2s+15)+(V-[(100/s)+30])/(3s+10)=0.
6. The value of the voltage V in the circuit shown below is?

a) 40(s+7.5)/s(s+5) – 12(s+7.5)/(s-5)
b) 40(s+7.5)/s(s+5) – 12(s+7.5)/(s+5)
c) 40(s+7.5)/s(s+5) + 12(s+7.5)/(s-5)
d) 40(s+7.5)/s(s+5) + 12(s+7.5)/(s+5)
View Answer
Explanation: Solving for V yields V=40(s+7.5)/s(s+5) + 12(s+7.5)/(s+5). The current in the 3H inductor at t = 0 is 10A and the current in 2H inductor at t = 0 is zero.
7. The value of the voltage V after taking the partial fractions in the equation V/(2s+15)+(V-[(100/s)+30])/(3s+10)=0 is?

a) 12 + 60/s + 10/(s+5)
b) 12 – 60/s + 10/(s+5)
c) 12 – 60/s – 10/(s+5)
d) 12 + 60/s – 10/(s+5)
View Answer
Explanation: By taking the partial fractions we get V = 60/s-20/(s+5)+12+30/(s+5) and on solving the equation we get V = 12+60/s+10/(s+5).
8. Determine the voltage V after taking the inverse transform (12 + 60/s + 10/(s+5)).

a) 12δ(t)-(60-10e-5t)u(t)
b) 12δ(t)+(60+10e-5t)u(t)
c) 12δ(t)-(60+10e-5t)u(t)
d) 12δ(t)+(60-10e-5t)u(t)
View Answer
Explanation: By taking inverse transform of V = 12+60/s+10/(s+5) we have v=12δ(t)+(60+10e-5t)u(t) volts and we have to derive the expression for the current when t > 0.
9. The current equation for the circuit shown below is?

a) I=4/s-2/(s-5)
b) I=4/s-2/(s+5)
c) I=4/s+2/(s+5)
d) I=4/s+2/(s-5)
View Answer
Explanation: After the switch has been opened, the current in L1 is the same as the current in L1. The current equation is I=(100/s+30)/(5s+25). On solving we get I = 4/s-2/(s+5).
10. The value of the current after taking the inverse transform of the current is?

a) (4-2e5t)u(t)
b) (4-2e-5t)u(t)
c) (4+2e5t)u(t)
d) (4-2e-5t)u(t)
View Answer
Explanation: By taking the inverse transform of I = 4/s-2/(s+5) gives i = (4-2e-5t)u(t). Before the switch is opened,the current in L1 is 10A and the current in L2 is 0A.
Sanfoundry Global Education & Learning Series – Network Theory.
To practice all areas of Network Theory, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
