This set of Linear Integrated Circuit Multiple Choice Questions & Answers (MCQs) focuses on “First Order Low Pass Butterworth Filter”.
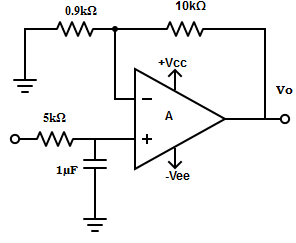
1. Find the voltage across the capacitor in the given circuit
a) VO= Vin/(1+0.0314jf)
b) VO= Vin×(1+0.0314jf)
c) VO= Vin+0.0314jf/(1+jf)
d) None of the mentioned
View Answer
Explanation: The voltage across the capacitor, VO= Vin/(1+j2πfRC)
=> VO= Vin/(1+j2π×5k×1µF×f)
=> VO= Vin/(1+0.0314jf).
2. Find the complex equation for the gain of the first order low pass butterworth filter as a function of frequency.
a) AF/[1+j(f/fH)].
b) AF/√ [1+j(f/fH)2].
c) AF×[1+j(f/fH)].
d) None of the mentioned
View Answer
Explanation: Gain of the filter, as a function of frequency is given as VO/ Vin=A F/(1+j(f/fH)).
3. Compute the pass band gain and high cut-off frequency for the first order high pass filter.
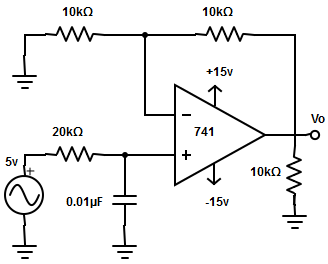
a) AF=11, fH=796.18Hz
b) AF=10, fH=796.18Hz
c) AF=2, fH=796.18Hz
d) AF=3, fH=796.18Hz
View Answer
Explanation: The pass band gain of the filter, AF =1+(RF/R1)
=>AF=1+(10kΩ/10kΩ)=2. The high cut-off frequency of the filter, fH=1/2πRC =1/(2π×20kΩ×0.01µF) =1/1.256×10-3 =796.18Hz.
4. Match the gain of the filter with the frequencies in the low pass filter
| Frequency | Gain of the filter |
| 1. f < fH | i. VO/Vin ≅ AF/√2 |
| 2. f=fH | ii. VO/Vin ≤ AF |
| 3. f>fH | iii. VO/Vin ≅ AF |
a)1-i,2-ii,3-iii
b)1-ii,2-iii,3-i
c)1-iii,2-ii,3-i
d)1-iii,2-i,3-ii
View Answer
Explanation: The mentioned answer can be obtained, if the value of frequencies are substituted in the gain magnitude equation |(Vo/Vin)|=AF/√(1+(f/fH)2).
5. Determine the gain of the first order low pass filter if the phase angle is 59.77o and the pass band gain is 7.
a) 3.5
b) 7
c) 12
d) 1.71
View Answer
Explanation: Given the phase angle, φ =-tan-1(f/fH)
=> f/fH=- φtan(φ) = -tan(59.77o)
=> f/fH= -1.716.
Substituting the above value in gain of the filter, |(VO/Vin)| = AF/√ (1+(f/fH)2) =7/√[1+(-1.716)2)] =7/1.986
=>|(VO/Vin)|=3.5.
6. In a low pass butterworth filter, the condition at which f=fH is called
a) Cut-off frequency
b) Break frequency
c) Corner frequency
d) All of the mentioned
View Answer
Explanation: The frequency, f=fH is called cut-off frequency, because the gain of the filter at this frequency is down by 3dB from 0Hz. Cut-off frequency is also called as break frequency, corner frequency or 3dB frequency.
7. Find the High cut-off frequency if the pass band gain of a filter is 10.
a) 70.7Hz
b) 7.07kHz
c) 7.07Hz
d) 707Hz
View Answer
Explanation: High cut-off frequency of a filter, fH=0.707×AF =0.707×10
=>fH=7.07Hz.
8. To change the high cutoff frequency of a filter. It is multiplied by R or C by a ratio of original cut-off frequency known as
a) Gain scaling
b) Frequency scaling
c) Magnitude scaling
d) Phase scaling
View Answer
Explanation: Once a filter is designed, it may sometimes be a need to change it’s cut-off frequency. The procedure used to convert an original cut-off frequency fH to a new cut-off frequency is called frequency scaling.
9. Using the frequency scaling technique, convert 10kHz cut-off frequency of the low pass filter to a cutoff frequency of 16kHz.(Take C=0.01µF and R=15.9kΩ)
a) 6.25kΩ
b) 9.94kΩ
c) 16kΩ
d) 1.59kΩ
View Answer
Explanation: To change a cut-off frequency from 10kHz to 16kHz,multiply 15.9kΩ resistor.
[Original cut-off frequency/New cut-off frequency] =10kHz/16kHz =0.625.
∴ R =0.625×15.9kΩ =9.94kΩ. However 9.94kΩ is not a standard value. So, a potentiometer of 10kΩ is taken and adjusted to 9.94kΩ.
10. Find the difference in gain magnitude for a filter ,if it is the response obtained for frequencies f1=200Hz and f2=3kHz. Specification: AF=2 and fH=1kHz.
a) 4.28 dB
b) 5.85 dB
c) 1.56 dB
d) None of the mentioned
View Answer
Explanation: When f1=200Hz, VO(1)/Vin =AF/√ [1+(f/fH)2] =2/√ [1+(200/1kHz) 2] =2/1.0198.
=> VO(1)/Vin =1.96
=>20log|(VO/Vin)|=5.85dB.
When f=700Hz, VO(2)/Vin= 2/√ [1+(700/1kHz) 2] =2/1.22=1.638.
=> VO(2)/Vin =20log|(VO/Vin|=20log(1.638) = 4.28.
Therefore, the difference in the gain magnitude is given as VO(1)/Vin-VO(2)/Vin =5.85-4.28 =1.56 dB.
11. Design a low pass filter at a cut-off frequency 1.6Hz with a pass band gain of 2.
a)
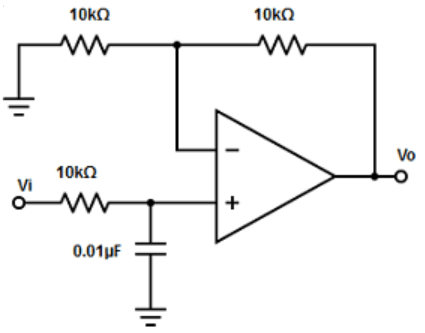
b)
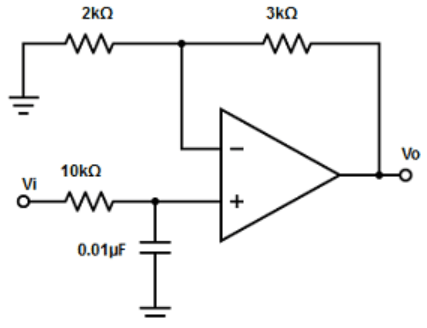
c)
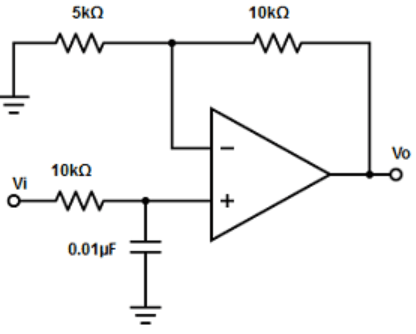
d)
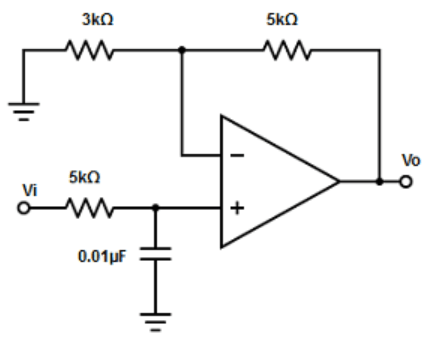
View Answer
Explanation: From the answer, it is clear that all the C values are the same . Therefore, c= 0.01µF
Given, fH = 1kHz,
=> R= 1/(2πCfm) = 1/2π×0.01µF×1kHz
R= 9.9kΩ ≅ 10kΩ. Since the pass band gain is 2.
=> 2=1+ (RF/R1). Therefore, RF and R1 must be equal.
Sanfoundry Global Education & Learning Series – Linear Integrated Circuits.
To practice all areas of Linear Integrated Circuits, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
