This set of Digital Signal Processing Multiple Choice Questions & Answers (MCQs) focuses on “IIR Filter Design by Approximation of Derivatives”.
1. An analog filter can be converted into digital filter by approximating the differential equation by an equivalent difference equation.
a) True
b) False
View Answer
Explanation: One of the simplest methods for converting an analog filter into digital filter is to approximate the differential equation by an equivalent difference equation.
2. Which of the following is the backward difference for the derivative of y(t) with respect to ‘t’ for t=nT?
a) [y(n)+y(n+1)]/T
b) [y(n)+y(n-1)]/T
c) [y(n)-y(n+1)]/T
d) [y(n)-y(n-1)]/T
View Answer
Explanation: For the derivative dy(t)/dt at time t=nT, we substitute the backward difference [y(nT)-y(nT-T)]/T. Thus
dy(t)/dt =[y(nT)-y(nT-T)]/T
=[y(n)-y(n-1)]/T
where T represents the sampling interval and y(n)=y(nT).
3. Which of the following is true relation among s-domain and z-domain?
a) s=(1+z-1)/T
b) s=(1+z )/T
c) s=(1-z-1)/T
d) None of the mentioned
View Answer
Explanation: The analog differentiator with output dy(t)/dt has the system function H(s)=s, while the digital system that produces the output [y(n)-y(n-1)]/T has the system function H(z) =(1-z-1)/T. Thus the relation between s-domain and z-domain is given as
s=(1-z-1)/T.
4. What is the second difference that is used to replace the second order derivate of y(t)?
a) [y(n)-2y(n-1)+y(n-2)]/T
b) [y(n)-2y(n-1)+y(n-2)]/T2
c) [y(n)+2y(n-1)+y(n-2)]/T
d) [y(n)+2y(n-1)+y(n-2)]/T2
View Answer
Explanation: We know that dy(t)/dt =[ y(n)-y(n-1)]/T
Second order derivative of y(t) is d(dy(t)/dt)/dt=[y(n)-2y(n-1)+y(n-2)]/T2.
5. Which of the following in z-domain is equal to s-domain of second order derivate?
a) \((\frac{1-z^{-1}}{T})^2\)
b) \((\frac{1+z^{-1}}{T})^2\)
c) \((\frac{1+z^{-1}}{T})^{-2}\)
d) None of the mentioned
View Answer
Explanation: We know that for a second order derivative
d2y(t)/dt2=[y(n)-2y(n-1)+y(n-2)]/T2
=>s2 = \(\frac{1-2z^{-1}+z^{-2}}{T^2} = (\frac{1-z^{-1}}{T})^2\)
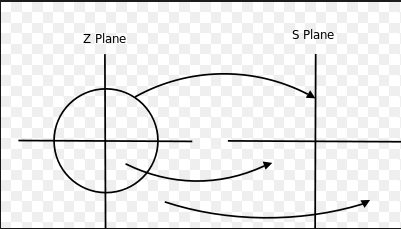
6. If s=jΩ and if Ω varies from -∞ to ∞, then what is the corresponding locus of points in z-plane?
a) Circle of radius 1 with centre at z=0
b) Circle of radius 1 with centre at z=1
c) Circle of radius 1/2 with centre at z=1/2
d) Circle of radius 1 with centre at z=1/2
View Answer
Explanation: We know that
s=(1-z-1)/T
=> z=1/(1-sT)
Given s= jΩ => z = 1/(1- jΩT)
Thus from the above equation if Ω varies from -∞ to ∞, then the corresponding locus of points in z-plane is a circle of radius 1/2 with centre at z=1/2.
7. Which of the following mapping is true between s-plane and z-domain?
a) Points in LHP of the s-plane into points inside the circle in z-domain
b) Points in RHP of the s-plane into points outside the circle in z-domain
c) Points on imaginary axis of the s-plane into points onto the circle in z-domain
d) All of the mentioned
View Answer
Explanation: The below diagram explains the given question
8. This mapping is restricted to the design of low pass filters and band pass filters having relatively small resonant frequencies.
a) True
b) False
View Answer
Explanation: The possible location of poles of the digital filter are confined to relatively small frequencies and as a consequence, the mapping is restricted to the design of low pass filters and band pass filters having relatively small resonant frequencies.
9. Which of the following filter transformation is not possible?
a) High pass analog filter to low pass digital filter
b) High pass analog filter to high pass digital filter
c) Low pass analog filter to low pass digital filter
d) None of the mentioned
View Answer
Explanation: We know that only low pass and band pass filters with low resonant frequencies in the digital can be designed. So, it is not possible to transform a high pass analog filter into a corresponding high pass digital filter.
10. It is possible to map the jΩ-axis into the unit circle.
a) True
b) False
View Answer
Explanation: By proper choice of the coefficients of {αk}, it is possible to map the jΩ-axis into the unit circle.
Sanfoundry Global Education & Learning Series – Digital Signal Processing.
To practice all areas of Digital Signal Processing, here is complete set of 1000+ Multiple Choice Questions and Answers.
