This set of Digital Signal Processing Multiple Choice Questions & Answers (MCQs) focuses on “Inversion of Z Transform”.
1. Which of the following method is used to find the inverse z-transform of a signal?
a) Counter integration
b) Expansion into a series of terms
c) Partial fraction expansion
d) All of the mentioned
View Answer
Explanation: All the methods mentioned above can be used to calculate the inverse z-transform of the given signal.
2. What is the inverse z-transform of X(z)=\(\frac{1}{1-1.5z^{-1}+0.5z^{-2}}\) if ROC is |z|>1?
a) {1,3/2,7/4,15/8,31/16,….}
b) {1,2/3,4/7,8/15,16/31,….}
c) {1/2,3/4,7/8,15/16,31/32,….}
d) None of the mentioned
View Answer
Explanation: Since the ROC is the exterior circle, we expect x(n) to be a causal signal. Thus we seek a power series expansion in negative powers of ‘z’. By dividing the numerator of X(z) by its denominator, we obtain the power series
X(z)=\(\frac{1}{1-1.5z^{-1}+0.5z^{-2}}=1+\frac{3}{2}z^{-1}+\frac{7}{4}z^{-2}+\frac{15}{8}z^{-3}+\frac{31}{16}z^{-4}+…\)
So, we obtain x(n)= {1,3/2,7/4,15/8,31/16,….}.
3. What is the inverse z-transform of X(z)=\(\frac{1}{1-1.5z^{-1}+0.5z^{-2}}\) if ROC is |z| < 0.5?
a) {….62,30,14,6,2}
b) {…..62,30,14,6,2,0,0}
c) {0,0,2,6,14,30,62…..}
d) {2,6,14,30,62…..}
View Answer
Explanation: In this case the ROC is the interior of a circle. Consequently, the signal x(n) is anti causal. To obtain a power series expansion in positive powers of z, we perform the long division in the following way:
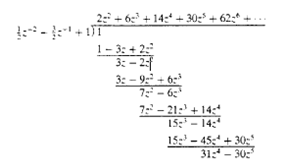
Thus X(z)=\(\frac{1}{1-1.5z^{-1}+0.5z^{-2}}=2z^2+6z^3+14z^4+30z^5+62z^6+…\) In this case x(n)=0 for n≥0.Thus we obtain x(n)= {…..62,30,14,6,2,0,0}
4. What is the inverse z-transform of X(z)=log(1+az-1) |z|>|a|?
a) x(n)=(-1)n+1 \(\frac{a^{-n}}{n}\), n≥1; x(n)=0, n≤0
b) x(n)=(-1)n-1 \(\frac{a^{-n}}{n}\), n≥1; x(n)=0, n≤0
c) x(n)=(-1)n+1 \(\frac{a^{-n}}{n}\), n≥1; x(n)=0, n≤0
d) None of the mentioned
View Answer
Explanation: Using the power series expansion for log(1+x), with |x|<1, we have
X(z)=\(\sum_{n=1}^∞ \frac{(-1)^{n+1} a^n z^{-n}}{n}\)
Thus
x(n)=(-1)n+1 \(\frac{a^n}{n}\), n≥1
=0, n≤0.
5. What is the proper fraction and polynomial form of the improper rational transform
X(z)=\(\frac{1+3z^{-1}+\frac{11}{6} z^{-2}+\frac{1}{3} z^{-3}}{1+\frac{5}{6} z^{-1}+\frac{1}{6} z^{-2}}\)?
a) 1+2z-1+\(\frac{\frac{1}{6}z^{-1}}{1+\frac{5}{6} z^{-1}+\frac{1}{6} z^{-2}}\)
b) 1-2z-1+\(\frac{\frac{1}{6} z^{-1}}{1+\frac{5}{6} z^{-1}+\frac{1}{6} z^{-2}}\)
c) 1+2z-1+\(\frac{\frac{1}{3} z^{-1}}{1+\frac{5}{6} z^{-1}+\frac{1}{6} z^{-2}}\)
d) 1+2z-1–\(\frac{\frac{1}{6} z^{-1}}{1+\frac{5}{6} z^{-1}+\frac{1}{6} z^{-2}}\)
View Answer
Explanation: First, we note that we should reduce the numerator so that the terms z-2 and z-3 are eliminated. Thus we should carry out the long division with these two polynomials written in the reverse order. We stop the division when the order of the remainder becomes z-1. Then we obtain
X(z)=1+2z-1+\(\frac{\frac{1}{6} z^{-1}}{1+\frac{5}{6} z^{-1}+\frac{1}{6} z^{-2}}\).
6. What is the partial fraction expansion of the proper function X(z)=\(\frac{1}{1-1.5z^{-1}+0.5z^{-2}}\)?
a) \(\frac{2z}{z-1}-\frac{z}{z+0.5}\)
b) \(\frac{2z}{z-1}+\frac{z}{z-0.5}\)
c) \(\frac{2z}{z-1}+\frac{z}{z+0.5}\)
d) \(\frac{2z}{z-1}-\frac{z}{z-0.5}\)
View Answer
Explanation: First we eliminate the negative powers of z by multiplying both numerator and denominator by z2.
Thus we obtain X(z)=\(\frac{z^2}{z^2-1.5z+0.5}\)
The poles of X(z) are p1=1 and p2=0.5. Consequently, the expansion will be
\(\frac{X(z)}{z} = \frac{z}{(z-1)(z-0.5)} = \frac{2}{(z-1)} – \frac{1}{(z-0.5)}\)
(obtained by applying partial fractions)
=>X(z)=\(\frac{2z}{(z-1)}-\frac{z}{(z-0.5)}\).
7. What is the partial fraction expansion of X(z)=\(\frac{1+z^{-1}}{1-z^{-1}+0.5z^{-2}}\)?
a) \(\frac{z(0.5-1.5j)}{z-0.5-0.5j} – \frac{z(0.5+1.5j)}{z-0.5+0.5j}\)
b) \(\frac{z(0.5-1.5j)}{z-0.5-0.5j} + \frac{z(0.5+1.5j)}{z-0.5+0.5j}\)
c) \(\frac{z(0.5+1.5j)}{z-0.5-0.5j} – \frac{z(0.5-1.5j)}{z-0.5+0.5j}\)
d) \(\frac{z(0.5+1.5j)}{z-0.5-0.5j} + \frac{z(0.5-1.5j)}{z-0.5+0.5j}\)
View Answer
Explanation: To eliminate the negative powers of z, we multiply both numerator and denominator by z2. Thus,
X(z)=\(\frac{z(z+1)}{z^{-2}-z+0.5}\)
The poles of X(z) are complex conjugates p1=0.5+0.5j and p2=0.5-0.5j
Consequently the expansion will be
X(z)= \(\frac{z(0.5-1.5j)}{z-0.5-0.5j} + \frac{z(0.5+1.5j)}{z-0.5+0.5j}\).
8. What is the partial fraction expansion of X(z)=\(\frac{1}{(1+z^{-1})(1-z^{-1})^2}\)?
a) \(\frac{z}{4(z+1)} + \frac{3z}{4(z-1)} + \frac{z}{2(z+1)^2}\)
b) \(\frac{z}{4(z+1)} + \frac{3z}{4(z-1)} – \frac{z}{2(z+1)^2}\)
c) \(\frac{z}{4(z+1)} + \frac{3z}{4(z-1)} + \frac{z}{2(z-1)^2}\)
d) \(\frac{z}{4(z+1)} + \frac{z}{4(z-1)} + \frac{z}{2(z+1)^2}\)
View Answer
Explanation: First we express X(z) in terms of positive powers of z, in the form X(z)=\(\frac{z^3}{(z+1)(z-1)^2}\)
X(z) has a simple pole at z=-1 and a double pole at z=1. In such a case the approximate partial fraction expansion is
\(\frac{X(z)}{z} = \frac{z^2}{(z+1)(z-1)^2} = \frac{A}{z+1} + \frac{B}{z-1} + \frac{C}{(z-1)^2}\)
On simplifying, we get the values of A, B and C as 1/4, 3/4 and 1/2 respectively.
Therefore, we get \(\frac{z}{4(z+1)} + \frac{3z}{4(z-1)} + \frac{z}{2(z-1)^2}\).
9. What is the inverse z-transform of X(z)=\(\frac{1}{1-1.5z^{-1}+0.5z^{-2}}\) if ROC is |z|>1?
a) (2-0.5n)u(n)
b) (2+0.5n)u(n)
c) (2n-0.5n)u(n)
d) None of the mentioned
View Answer
Explanation: The partial fraction expansion for the given X(z) is
\(X(z)= \frac{2z}{z-1}-\frac{z}{z-0.5}\)
In case when ROC is |z|>1, the signal x(n) is causal and both the terms in the above equation are causal terms. Thus, when we apply inverse z-transform to the above equation, we get
x(n)=2(1)nu(n)-(0.5)nu(n)=(2-0.5n)u(n).
10. What is the inverse z-transform of X(z)=\(\frac{1}{1-1.5z^{-1}+0.5z^{-2}}\) if ROC is |z|<0.5?
a) [-2-0.5n]u(n)
b) [-2+0.5n]u(n)
c) [-2+0.5n]u(-n-1)
d) [-2-0.5n]u(-n-1)
View Answer
Explanation: The partial fraction expansion for the given X(z) is
\(X(z)= \frac{2z}{z-1}-\frac{z}{z-0.5}\)
In case when ROC is |z|<0.5, the signal is anti causal. Thus both the terms in the above equation are anti causal terms. So, if we apply inverse z-transform to the above equation we get
x(n)= [-2+0.5n]u(-n-1).
11. What is the inverse z-transform of X(z)=\(\frac{1}{1-1.5z^{-1}+0.5z^{-2}}\) if ROC is 0.5<|z|<1?
a) -2u(-n-1)+(0.5)nu(n)
b) -2u(-n-1)-(0.5)nu(n)
c) -2u(-n-1)+(0.5)nu(-n-1)
d) 2u(n)+(0.5)nu(-n-1)
View Answer
Explanation: The partial fraction expansion of the given X(z) is
\(X(z)= \frac{2z}{z-1}-\frac{z}{z-0.5}\)
In this case ROC is 0.5<|z|<1 is a ring, which implies that the signal is two sided. Thus one of the signal corresponds to a causal signal and the other corresponds to an anti causal signal. Obviously, the ROC given is the overlapping of the regions |z|>0.5 and |z|<1. Hence the pole p2=0.5 provides the causal part and the pole p1=1 provides the anti causal part. SO, if we apply the inverse z-transform we get
x(n)= -2u(-n-1)-(0.5)nu(n).
12. What is the causal signal x(n) having the z-transform X(z)=\(\frac{1}{(1+z^{-1})(1-z^{-1})^2}\)?
a) [1/4(-1)n+3/4-n/2]u(n)
b) [1/4(-1)n+3/4-n/2]u(-n-1)
c) [1/4+3/4(-1)n-n/2]u(n)
d) [1/4(-1)n+3/4+n/2]u(n)
View Answer
Explanation: The partial fraction expansion of X(z) is \(X(z) = \frac{z}{4(z+1)} + \frac{3z}{4(z-1)} + \frac{z}2{(z-1)^2}\)
When we apply the inverse z-transform for the above equation, we get
x(n)=[1/4(-1)n+3/4+n/2]u(n).
Sanfoundry Global Education & Learning Series – Digital Signal Processing.
To practice all areas of Digital Signal Processing, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
