This set of Digital Signal Processing Questions & Answers for freshers focuses on “Efficient Computation of DFT FFT Algorithms”.
1. If we split the N point data sequence into two N/2 point data sequences f1(n) and f2(n) corresponding to the even numbered and odd numbered samples of x(n), then such an FFT algorithm is known as decimation-in-time algorithm.
a) True
b) False
View Answer
Explanation: Let us consider the computation of the N=2v point DFT by the divide and conquer approach. We select M=N/2 and L=2. This selection results in a split of N point data sequence into two N/2 point data sequences f1(n) and f2(n) corresponding to the even numbered and odd numbered samples of x(n), respectively, that is
f1(n)=x(2n)
f2(n)=x(2n+1), n=0,1,2…N/2-1
Thus f1(n) and f2(n) are obtained by decimating x(n) by a factor of 2, and hence the resulting FFT algorithm is called a decimation-in-time algorithm.
2. If we split the N point data sequence into two N/2 point data sequences f1(n) and f2(n) corresponding to the even numbered and odd numbered samples of x(n) and F1(k) and F2(k) are the N/2 point DFTs of f1(k) and f2(k) respectively, then what is the N/2 point DFT X(k) of x(n)?
a) F1(k)+F2(k)
b) F1(k)-WNk F2(k)
c) F1(k)+WNk F2(k)
d) None of the mentioned
View Answer
Explanation: From the question, it is given that
f1(n)=x(2n)
f2(n)=x(2n+1), n=0,1,2…N/2-1
X(k)=\(\sum_{n=0}^{N-1} x(n) W_N^{kn}\), k=0,1,2..N-1
=\(\sum_{n \,even} x(n) W_N^{kn}+\sum_{n \,odd} x(n) W_N^{kn}\)
=\(\sum_{m=0}^{(\frac{N}{2})-1} x(2m)W_N^{2km}+\sum_{m=0}^{(\frac{N}{2})-1} x(2m+1) W_N ^{k(2m+1)}\)
=\(\sum_{m=0}^{(\frac{N}{2})-1} f_1(m) W_{N/2}^{km} + W_N^k \sum_{m=0}^{(N/2)-1} f_2(m) W_{(\frac{N}{2})}^{km}\)
X(k)=F1(k)+ WNk F2(k).
3. If X(k) is the N/2 point DFT of the sequence x(n), then what is the value of X(k+N/2)?
a) F1(k)+F2(k)
b) F1(k)-WNk F2(k)
c) F1(k)+WNk F2(k)
d) None of the mentioned
View Answer
Explanation: We know that, X(k) = F1(k)+WNk F2(k)
We know that F1(k) and F2(k) are periodic, with period N/2, we have F1(k+N/2) = F1(k) and F2(k+N/2)= F2(k). In addition, the factor WNk+N/2 = -WNk.
Thus we get, X(k+N/2)= F1(k)- WNk F2(k).
4. How many complex multiplications are required to compute X(k)?
a) N(N+1)
b) N(N-1)/2
c) N2/2
d) N(N+1)/2
View Answer
Explanation: We observe that the direct computation of F1(k) requires (N/2)2 complex multiplications. The same applies to the computation of F2(k). Furthermore, there are N/2 additional complex multiplications required to compute WNk. Hence it requires N(N+1)/2 complex multiplications to compute X(k).
5. The total number of complex multiplications required to compute N point DFT by radix-2 FFT is?
a) (N/2)log2N
b) Nlog2N
c) (N/2)logN
d) None of the mentioned
View Answer
Explanation: The decimation of the data sequence should be repeated again and again until the resulting sequences are reduced to one point sequences. For N=2v, this decimation can be performed v=log2N times. Thus the total number of complex multiplications is reduced to (N/2)log2N.
6. The total number of complex additions required to compute N point DFT by radix-2 FFT is?
a) (N/2)log2N
b) Nlog2N
c) (N/2)logN
d) None of the mentioned
View Answer
Explanation: The decimation of the data sequence should be repeated again and again until the resulting sequences are reduced to one point sequences. For N=2v, this decimation can be performed v=log2N times. Thus the total number of complex additions is reduced to Nlog2N.
7. The following butterfly diagram is used in the computation of __________
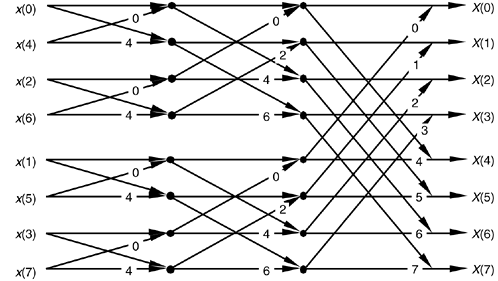
a) Decimation-in-time FFT
b) Decimation-in-frequency FFT
c) All of the mentioned
d) None of the mentioned
View Answer
Explanation: The above given diagram is the basic butterfly computation in the decimation-in-time FFT algorithm.
8. For a decimation-in-time FFT algorithm, which of the following is true?
a) Both input and output are in order
b) Both input and output are shuffled
c) Input is shuffled and output is in order
d) Input is in order and output is shuffled
View Answer
Explanation: In decimation-in-time FFT algorithm, the input is taken in bit reversal order and the output is obtained in the order.
9. The following butterfly diagram is used in the computation of __________
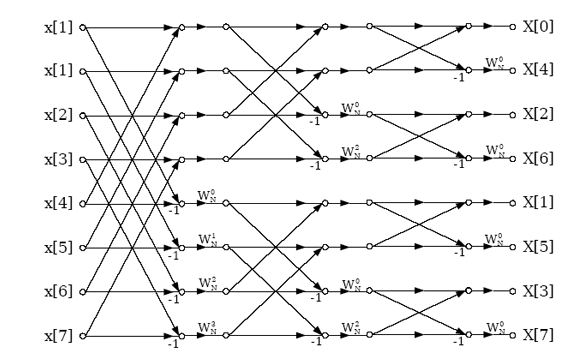
a) Decimation-in-time FFT
b) Decimation-in-frequency FFT
c) All of the mentioned
d) None of the mentioned
View Answer
Explanation: The above given diagram is the basic butterfly computation in the decimation-in-frequency FFT algorithm.
10. For a decimation-in-time FFT algorithm, which of the following is true?
a) Both input and output are in order
b) Both input and output are shuffled
c) Input is shuffled and output is in order
d) Input is in order and output is shuffled
View Answer
Explanation: In decimation-in-frequency FFT algorithm, the input is taken in order and the output is obtained in the bit reversal order.
Sanfoundry Global Education & Learning Series – Digital Signal Processing.
To practice all areas of Digital Signal Processing for freshers, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
