Theory of Computation - Nondeterministic Finite Automata (NFA) - Definitions, Programming, Examples

Nondeterministic means choice of moves for automata. In non-deterministic finite automata we are allowed a set of possible moves. The definition of nondeterministic automata is similar to that of deterministic finite automata but with one difference, the transition function. A nondeterministic finite automata is s 5-tuple ( Q, Σ, δ, F q₀), where
Q: is a non-empty finite set of states present in the finite control.
Σ: is a non-empty finite set of input symbols which can be passed on to the finite state machine
q₀: is a starting state, q₀ ϵ Q
F: is a non-empty set of final states or accepting states, set of final states is a subset of Q.
δ: is a function called transition function that takes two arguments a state and a input symbol and it returns a subset of Q that is,
Q x (Σ U {є})->2^Q
2^Q is the power set of Q (the set of subsets of Q).

The language accepted by a NFA is regular just as in case of a DFA . There are some languages that cannot be represented by a DFA but can be represented as an NFA for example (11 + 110)*0 cannot be represented by a DFA. The non-deterministic finite automata can be thought of as a machine making decisions. The given expression is shown in the form an automaton in the figure. There are two possible moves from the start state on input 1. Nondeterminism means that the behavior of the language is unpredictable. On a given input we can for a state we may have choice of making the move to more than one state unlike in deterministic finite automata where transition to only a single state is permitted for a given input symbol.

The transition graph for a NFA is constructed in the same way as a DFA. For the transition table there may be multiple states in a column for a given state. The transition diagram for the NFA for (11 + 110)*0 would be :

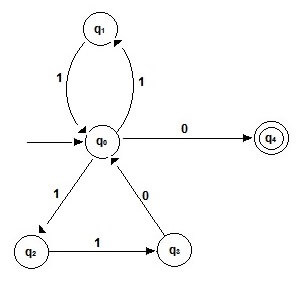
Question 1: Design a NFA for the following language:

L = (ab)* (ba)* U aa*
L = all strings over {0, 1} that have at least two consecutive 0’s or 1’s.

View Answer

Answer:

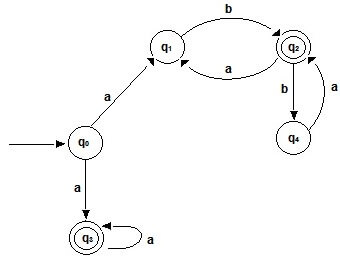
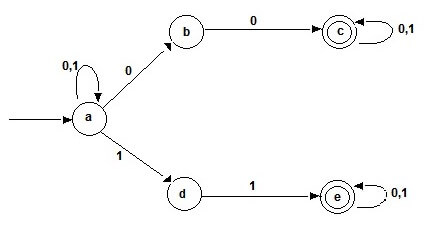
Question 2: Design a NFA and a DFA for the language L = (ab U aba)*.
View Answer

The DFA for the language will be:

and the NFA would be :

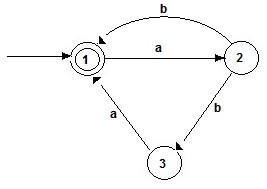
Question 3: Write a program to simulate a NFA. Run the code for the NFA (11 + 110)*0.

Answer:
A NFA can be simulated in many ways. The approach in the following program is to store all the possible current state for a given input symbol and after the final input test if the NFA ends up in a final state.
Here is source code of the C++ Program to simulate a nondeterministic finite automaton. The C++ program is successfully compiled and run on a Linux system. The program output is also shown below.

Subscribe Now: Automata Theory Newsletter | Important Subjects Newsletters

```
#include <iostream>
```
```
#include <string>
```
```
#include <cstring>
```
```
#include <stdlib.h>
```
```
using namespace std;
```
```
 
```
```
class Transition{
```
```
    public:
```
```
    string str;
```
```
    int cnt;
```
```
    string * list;
```
```
 
```

    // a function to tokenize the string and store it in the list

```
    void strTokenize() {
```
```
        comma ();
```

        char *cstr = new char[str.length() + 1];

```
        strcpy(cstr, str.c_str());
```

        char *p = strtok(cstr, ",");// in strtok() first parameter has t0 be a character array

```
        int i = 0;
```
```
        list = new string[cnt];
```

        // tokenize the string and create a list of states for that symbol

```
        while (p != 0) {
```
```
            list[i] = p;
```
```
            i++;
```
```
            p = strtok(NULL, ",");
```
```
        }
```
```
    }
```
```
 
```
```
    void showList(){
```
```
        for (int i=0; i < cnt; i++)
```
```
            cout << list[i] << " ";
```
```
    }
```
```
 
```
```
    private:
```

    // function to count the comma (',') in the entered set of states

```
    void comma() {
```
```
        cnt = 1;
```
```
	size_t found = str.find(',');
```
```
        while (found != string::npos) {
```
```
            cnt++;
```

            found = str.find(',', found + 1);

```
    	}
```
```
     }
```
```
 
```
```
};
```
```
 
```
```
int main() {
```
```
    Transition **trans;
```

    string *states, *final, str, input, temp[nos], current[nos];

```
    char *alf;
```

    int nos, nofs, noa, i, j, k, x, y, z, f, flag, cnt, temp_last, curr_last;

```
 
```

    cout << "Enter the total number of states and the "

```
    << "number of final states :\n";
```
```
    cin >> nos >> nofs;
```
```
    states = new string[nos];
```
```
    final = new string[nofs];
```

    cout << "Enter the states (enter the start state first)\n";

```
    for (i = 0; i < nos; i++)
```
```
        cin >> states[i];
```
```
	cout << "Enter the final states\n";
```
```
    for (i = 0; i < nofs; i++)
```
```
        cin >> final[i];
```
```
 
```

    cout << "Enter the number of symbols in the alphabet : ";

```
    cin >> noa;
```
```
    alf = new char[noa];
```

    cout << "Enter the symbols for the alphabet:\n";

```
    for (i = 0; i < noa; i++)
```
```
        cin >> alf[i];
```
```
 
```

    // allocating space for the transition table

```
    trans = new Transition*[nos];
```
```
    for (j = 0; j < nos; j++)
```
```
        trans[j] = new Transition[noa];
```
```
 
```

    // retrieving the information for transition table

    cout << "Enter the information for the transition table"

         << " (enter t when no move is possible from the given state) :\n";

```
    for (i = 0; i < nos; i++) {
```

	cout << "Write the transitions for state " << states[i] << endl;

```
        for (j = 0; j < noa; j++){
```

       	    cout << "On input symbol " << alf[j] << ": ";

```
	    cin >> trans[i][j].str;
```
```
            trans[i][j].strTokenize();
```
```
	}
```
```
    }
```

    cout << endl << "the transition table entered by you is :\n";

```
    for (i = 0; i < nos; i++) {
```
```
        for (j = 0; j < noa; j++) {
```
```
            trans[i][j].showList();
```
```
            cout << "\t\t";
```
```
        }
```
```
        cout<<endl;
```
```
    }
```
```
 
```

    // this array of strings will contain the states that are currently being considered

```
    while (true) {
```

        cout << "\nEnter the input string (enter exit to stop the program) : ";

```
        cin >> input;
```
```
        if (input == "exit")
```
```
            exit(0);
```
```
 
```
```
        curr_last = 0;
```

        current[curr_last] = states[0];// initialising the current state with the start state

        for (i = 0; i < input.length(); i++){

        // getting the index of the alphabet symbol

```
            for (j = 0; j < noa; j++)
```
```
                if (alf[j] == input[i])
```
```
                    break;
```
```
 
```

	    // processing of the input string by the NFA

```
 
```

        /*  first for an input we will pop off from the current

            then we will scan all the transitions from that state for the input symbol

            then we will add these transition to the temp variable if it was not previously present

            finally we will replace the values in current with the values in temp

            curr_last has to be updated accordingly

            index of the alphabet symbol is stored in j

            Transition is T[current_state_being scanned][j]

```
        */
```
```
 
```

        // to get the current states number scan states[k]

```
 
```
```
            temp_last = 0;
```
```
 
```

	    for (k = 0; k <= curr_last; k++) { //loop for scanning the transitions from every state in current

```
                if (current[k] == "t")
```
```
                    continue;
```
```
	        for (x = 0; x < nos; x++)
```

                    if (states[x] == current[k])

```
                        break;
```
```
                cnt = trans[x][j].cnt;
```

                for (y = 0; y < cnt; y++){// iterating the list of transitions

                    str = trans[x][j].list[y];

```
                    flag = 0;
```

                    for (z = 0; z < temp_last; z++){ // checking whether the state is already present in the temp[]

                        if (str == "t") {

```
                            flag = 1;
```
```
                            break;
```
```
                        }
```

                        if (temp[z] == str) {

```
                            flag = 1;
```
```
                            break;
```
```
                        }
```
```
                    }
```
```
                    if (flag == 0)
```

                        temp[temp_last++] = str;

```
                }
```

                // updating the current and curr_last

```
 
```
```
            }
```
```
 
```

            for (y = 0; y <= temp_last; y++)

```
                current[y] = temp[y];
```

            curr_last = temp_last - 1; // as the last increment was not required

```
        }
```
```
 
```
```
        f = 0;
```
```
        // loop checking for acceptance
```

        for (i = 0; i <= curr_last; i++) {

```
            for(j = 0; j < nofs; j++)
```

                if (final[j] == current[i]) {

                    cout<<"\n----The string has been accepted----\n";

```
                    f = 1;
```
```
                    break;
```
```
                }
```
```
            if (f == 1) break;
```
```
        }
```
```
 
```
```
    if (f == 0)
```

        cout<<"\n----The string has been rejected----\n";

```
}
```
```
return 0;
```
```
}
```

Output

Enter the total number of states and the number of final states
5
1
Enter the states (enter the start state first)
q0
q1
q2
q3 
q4
Enter the final states
q4
Enter the number of symbols in the alphabet : 2
Enter the symbols for the alphabet:
0
1
Enter the information for the transition table (enter t when no move is possible from the given state):
Write the transitions for state q0
On input symbol 0: q4
On input symbol 1: q1,q2
Write the transitions for state q1
On input symbol 0: t 
On input symbol 1: q0
Write the transitions for state q2
On input symbol 0: t
On input symbol 1: q3 
Write the transitions for state q3
On input symbol 0: q0
On input symbol 1: t
Write the transitions for state q4
On input symbol 0: t
On input symbol 1: t
 
the transition table entered by you is :
q4 		q1 q2 		
t 		q0 		
t 		q3 		
q0 		t 		
t 		t 		
 
Enter the input string (enter exit to stop the program) : 1101101
 
----The string has been rejected----
 
Enter the input string (enter exit to stop the program) : 10101
 
----The string has been rejected----
 
Enter the input string (enter exit to stop the program) : 1101110
 
----The string has been rejected----
 
Enter the input string (enter exit to stop the program) : 1101100
 
----The string has been accepted----
 
Enter the input string (enter exit to stop the program) : 11110
 
----The string has been accepted----
 
Enter the input string (enter exit to stop the program) : 111100
 
----The string has been accepted----
 
Enter the input string (enter exit to stop the program) : exit

Sanfoundry Global Education & Learning Series – 100+ Theory of Computation Tutorials.

If you wish to look at all Tutorials and their examples, go to Theory of Computation Tutorials.

If you find any mistake above, kindly email to [email protected]

« Prev - Theory of Computation – Designing and Programming a DFA

» Next - Theory of Computation – Nondeterministic Finite Automata with Null Transitions

Related Posts:

Recommended Articles: